2020-01-15
149
Изучить соответствующие разделы курса по конспекту лекции или учебнику.
Рассмотрим, как, используя векторную диаграмму, можно определить параметры цепи напряжения или тока.
Пусть задана схема.
Рис.1
В цепи измерены действующие значения напряжений 
и действующие значения токов 
и 
. Необходимо определить ток 
и параметры цепи.
Строим векторную диаграмму следующим образом. Выбираем масштабы для напряжений и токов. Затем задаем вектор напряжения 
. Из точки (b) радиусом 
проводим окружность, а из точки (с) радиусом 
делаем засечки на окружности радиуса 
. Получаем точки 
и 
на векторной диаграмме, и следовательно, положение векторов напряжений 
, 
. Строим вектора токов. Направление тока совпадает с направлением напряжения 
так как на участке 
находится активное сопротивление R. Из точки 
откладываем вектор тока 
. Направление тока 
неизвестно, но известна его величина. Из точки проводим окружность радиуса 
.
Через конец вектора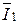 
проводим перпендикуляр 
. Тогда отрезок 
будет ток 
, а отрезок 
- ток 
, так как в заданной схеме 
.
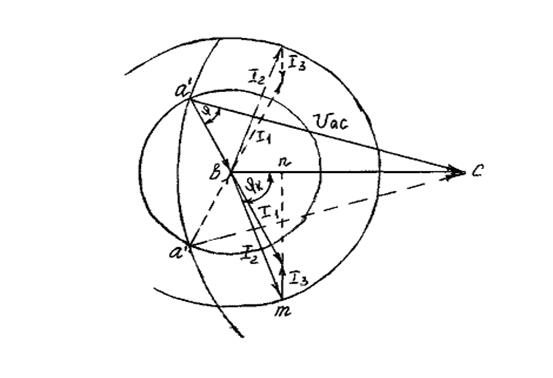
Рис.2
Теперь из векторной диаграммы можно определить угол сдвига фаз 
на входе цепи, т.е. между напряжениями 
и током 
.
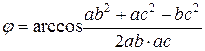
Угол сдвига фаз на катушке 
будет равен:
.
Тогда параметры цепи определяются следующим образом:
; 
; 
; 
.
Емкость 
, индуктивность 
, где 
эквивалентное активное сопротивление всей цепи 
, и эквивалентное реактивное 
.
Отметим одну особенность при построении векторной диаграммы. При пересечении окружностей радиусов 
и 
получим два положения для точки а. Положение 
не удовлетворяет решению, так как фазовые углы сдвига не соответствуют характеру нагрузки на участках цепи. На диаграмме ток 
отстает от напряжения, а должен опережать, так это ток емкости. Ток 
опережает напряжение 
, а должен отставать, так как это ток в индуктивности. В данной схеме удовлетворяет решению положение точки 
.
