2020-01-14
548
Теперь перейдем к гауссовским квадратурам – семейству правил интегрирования, основанных на неравномерном разбиении основного интервала интегрирования. Вообще, метод гаусса с n точками точен для полиномов степени 2 n – 1. В функции gauss3 (листинг1.6.) основной трехточечный алгоритм Гаусса применяется к каждой из n равных частей интервала. Для интервала [-1,1] узлами квадратурной формулы являются нули полинома Лежандра третьей степени P 3 = (5 x 3 – 3 x)/2, а коэффициенты выбираются специальным образом.
Листинг 1.6. Функция gauss3 модуля integral
Function gaus3(F:real_fun; x0,x1:real; n:word):real;
var
t,sum,x,z,dx:real;
i,k:word;
gzero,gweight:array[1..3] of real;
procedure initialize_constants;
var
s,t:real;
j:word;
begin
gzero[1]:=-sqrt(0.6);
gzero[2]:=0.0;
gzero[3]:=sqrt(0.6);
gweight[1]:=5.0/9.0;
gweight[2]:=8.0/9.0
gweight[3]:=5.0/9.0;
for j:=1 to 3 do
begin
gzero[j]:=0.5*(1.0+gzero[j]);
gweight[j]:=0.5*gweight[j]);
end;
end; {initialize_constants}
begin {gauss3}
initialize_constants;
dx:=(x1-x0)/n;
x:=x0;
sum:=0.0;
for i:=0 to n-1 do
begin
t:=0.0;
for k:=1 to 3 do
begin
z:=x+dx*gzero[k];
t:=t+gweight[k]*F(z);
end;
sum:=sum+dx*t;
x:=x+dx;
|
|
|
end;
gauss3:=sum;
end;{gauss3}
Дадим некоторый обзор некоторых свойств полиномов Лежандра. Рекурсивное определение полиномов Лежандра приводилось ранее в этой работе. Они образуют ортогональное (но не ортонормированное)семейство на промежутке [-1,1], то есть
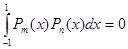, m ≠ n,
.
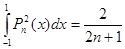Величина второго интеграла определяет нормировку для этих полиномов. Имеет место также следующее представление полиномов Лежандра:
.
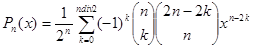Другая явная формула:
.
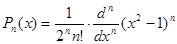Приведем несколько первых полиномов Лежандра:
P 0(x) = 1,
P 1(x) = x,
,
,
,
.
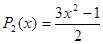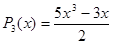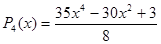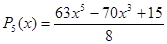Очевидно, что в общем случае полиномы Лежандра нечетной степени являются нечетными функциями, а четной степени – четными функциями.
Нам требуется найти нули полинома Pn (x). Важно здесь то, что эти нули являются простыми и принадлежат открытому интервалу (-1,1). Таким образом,
-1< x 1< x 2<…< xn <1, Pn (xj) = 0.
Соответствующая формула гаусовского интегрировании (с остатком) имеет следующий вид:
.
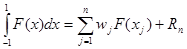В этой формуле
,
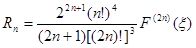Где 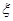-1 < 
<1.
Веса задаются несколькими эквивалентными формулами
.
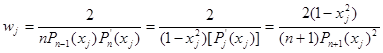Процедура compute_gauss_coeffs (листинг1.7). предназначена для вычисления нулей и весов квадратурной формулы Гаусса. Подпрограмма legendre_poly вычисляет значения Pn (x), Pn -1(x) и Pn ’(x). Последнее получается дифференцированием основной рекуррентной формулы для Pn (x):
.
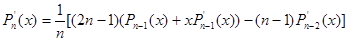Нули находятся предварительным делением интервала и применением метода секущих, после чего следует ньютоновские итерации, в которых используются значения производных. Затем применяется первая формула для весов, в которой вновь используются значения производных. Здесь zero – массив нулей полинома Лежандра n -й степени, а weight – массив соответствующих весов.
|
|
|
Метод вычислений нулей полинома заключается в том, чтобы поделить интервал [0,1] на маленькие подынтервалы и проверить каждый из них на изменение знака полинома. Если изменение знака имеет место, то однократное применение метода секущих позволяет достаточно хорошо определить положение нуля. Для уточнения этого значения применяется метод Ньютона. Для обработки интервала [-1,0] учитывается симметрия.
Листинг 1.7. Процедура compute_gauss_coeffs модуля integral
procedure compute_gauss_coeffs(deg:word);
const
eps=6.0e-20;
var
i,index:word;
P0k, P0k_1,D0k, P1k,P1k_1, D1k,
x0,x1,y,z,dx,x,u:real;
procedure legendre_poly(n:word; x:real; var Pk,Pk_1,Dk:real);
var
Pk_2,Dk_1,Dk_2:real;
i,j,k:word;
begin
If n=0 then
Begin
Pk:=1.0;
Dk:=0.0;
end
else
begin
Pk_1:=1.0;
Pk:=x;
Dk_1:=0.0;
Dk:=1.0;
i:==3;
j:=1;
for k:=2 to n do
begin
Pk_2:=Pk_1;
Pk_1:=Pk;
Dk_2:=Dk_1;
Dk_1:=Dk;
Pk:=(i*x*Pk_1-j*Pk_2)/k;
Dk:=(i*(Pk_1+x*Dk_1)-j*Dk_2)/k;
Inc(I,2);
Inc(j);
end;
end
end;{legendre_poly}
begin{computr_gauss_coeffs}
index:=(deg+1) div 2;
dx:=1.0/(10.0*deg);
x0:=0.0;
x1:=x0+dx;
if Odd(deg) then
begin
zero[index]:=0.0;
legendre_poly(deg,x0,P0k, P0k_1,D0k);
weight[index]:=2.0/(P0k_1*D0k*deg);
end;
for i:=0 to 10*deg-1 do
begin
x0:=x1;
x1:=x1+dx;
legendre_poly(deg,x0,P0k_1,D0k);
legendre_poly(deg,x1,P1k,P1k_1,D1k);
if P0k*P1k<=0.0 then
begin
x:=x0-P0k*dx/(P1k-P0k);
legendre_poly(deg,x,P0k,P0k_1,D0k);
u:=P0k/D0k;
y:=x-u;
while Abs(x-y)>=eps do
begin
if keyPressed then begin
writeln(‘>=eps loop:’,x:10:10,’ ‘, y:10:10,’ ‘,Abs(x-y):10);
readln;
end;
x:=y;
legendre_poly(deg,x,P0k,P0k_1,D0k);
u:=P0k/D0k;
y:=x-u;
end;
inc(index);
legendre_poly(deg,y,P0k,P0k_1,D0k);
zero[index]:=y;
weight[index]:=2.0/(P0k_1*D0k*deg);
if index=deg then
Break;
end;
end;
For i:=1 to deg div 2 do
begin
Zero[i]:=zero[deg-i+1];
Weight[i]:=weight[deg-i+1];
end;
end;{compute_gauss_coeffs}
В функции gauss (листинг 1.8.) запрограммирован один гауссовский шаг на заданном интервале. Конечно, серьезная прикладная программа будет делить интервал на меньшие подынтервалы, применять эту процедуру к каждому из них адаптивным способом.
Листинг1.8. Функция gauss модуля integral
Function gauss(F:real_fun;x0,x1:real;deg:word):real;
var
Index:word;
a,b,sum:real;
begin
a:=0.5*(x1-x0);
b:=0.5*(x1+x0);
sum:=0.0;
for index:=1 to deg do begin
sum:=sum+F(a*zero[index]+b)*weight[index];
if KeyPressed then
Halt;
end;
gauss:=a*sum;
end;
end.
Заключение
В данной работе были рассмотрены различные методы интегрирования определенных интегралов и их реализация на языке программирования высокого уровня Pascal. Таким образом было показано, что данный язык программирования возможно использовать для решения различных задач из области высшей математики и численных методов. В данной работе затронута лишь одна проблема – проблема вычисления интегралов, но Pascal позволяет решать и такие проблемы как: решение дифференциальных уравнений, вычисление с полиномами, решение нелинейных уравнений, вычисления связанные с линейной алгеброй.
Литература
1. Немнюгин С.А. Turbo Pascal, 2 - издание – С-П.: Питер, 2003-544 с.
2. Большой энциклопедический словарь: под редакцией Ю.В. Прохорова – М.: Большая Российская энциклопедия, 2000. – 845 с.
