Метод Ромберга и его реализация на языке Pascal

 

Интегрирование следующим методом – методом Ромберга – основано на правиле трапеций, использующем кусочно-линейное приближение для интегрируемой функции. Основной факт относительно погрешности в методе трапеций следующий.

Теорема. Пусть F (x) – гладкая функция на интервале [ a, b ], и этот интервал делится на т равных частей, каждая длиной h = 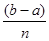. Пусть I (h) обозначает соответствующее приближение метода трапеций:

I (h) = ,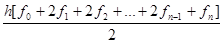

где f _i= F (a + jh) – значение интегрируемой функции в точке a + jh.

Тогда  

,

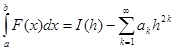Где a_k – некоторая константа.

Основное здесь то, что погрешность в методе трапеций может быть выражена рядом по четным степеням шага интегрирования h. Построим таблицу значений T _ik:

                                                   

                                     

                             

                                     

                                       

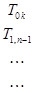
В нулевой строке T _{0 k} = I ((b – a)/2 k), так что T ₀₀, T ₀₁,… являются последовательными приближениями метода трапеций для интеграла, каждое с удвоенным по сравнению с предыдущим числом интервалов. Согласно приведенной выше теореме,

,

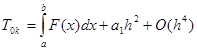где h =  ((b – a)/2 k.

Отсюда следует, что

,

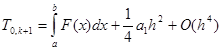Поэтому положим

.

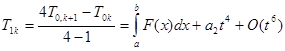В общем случае строим j-ю строку таблицы Ромберга по формуле

,

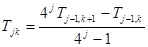а оценка погрешности имеет вид

,

где h = (b – a)/2 k.

Для работы понадобится не целая таблица, а только последняя вычисленная строка. Число точек выборки на каждом шаге удваивается. Обратите внимание на то, что функцию следует вычислять только в новых точках, которые являются средними точками предыдущих подынтервалов:

F ₀ + 2 F ₁ + 2 F ₂ + …+ 2 F _2n-1 + F _2n =

= (F ₀ + 2 F ₂ + 2 F ₄ + …+ 2 F _2n-2 + F _2n) + 2(F ₁ + F ₃ +…+ F _2n-1).

 

Таким образом, чтобы модифицировать предыдущее приближение, необходимо вычислить сумму значений функции в новых средних точках. Это делается в цикле со счетчиком k. Метод Ромберга реализован в функции romberg (листинг1.5).

Листинг 1.5. Функция romberg модуля integral

Function romberg (F:real_fun;x0,x1,eps,eta:real; min,max:word):real;

const

     abs_max=30;

var

p,dx,error,F_of_x0, F_of_x1, F_of_xk,

roundoff_error,integral_abs,tolerance,

previous_estimate,current_estimate,

mid_sum, temp_sum, mid_sum_abs:real;

table:array[0..abs_max] of real;

j,n:word;

k,r:longint;

done:Boolean;

denom:array[1..abs_max] of real;

begin

  p:=1.0;

  for k:=1 to abs_max do

begin

  p:=4.0*p;

denom[k]:=1.0/(p-1.0);

end;

dx:=x1-x0;

F_of_x0:=F(x0);

F_of_x1:=F(x1);

current_estimate:=0.0;

previos_estimate:=0.0;

done:=False;

table[0]:=0.5*dx*(F_of_x0+F_of_x1);

integral_abs:=0.5*Abs(dx)*(Abs(F_of_x0)+Abs(F_of_x1));

n:=1;

r:=1;

repeat

   dx:=0.5*dx;

   mid_sum:=0.0;

   mid_sum_abs:=0.0;

   roundoff_error:=0.0;

  for k:=1 to r do

begin

   F_of_xk:=F(x0+(2*k-1)*dx);

   mid_sum_abs:=mid_sum_abs+Abs(F_of_xk);

   F_of_xk:=F_of_xk+roundof_eroor;

  temp_sum:=mid_sum+F_of_xk;

  roundof_error:=(mid_sum-temp_sum)+F_of_xk;

  mid_sum:=temp_sum;

if KeyPressed then

                 Halt;

end;

    table[n]:=0.5*table[n-1]+dx*mid_sum;

    integral_abs:=0.5*integral_abs+Abs(dx)*mid_sum_abs;

    for j:=n-1 downto 0 do

    table[j]:=table[j+1]+denom[n-j]*(table[j+1]-table[j]);

     if n>=min then

begin

    tolerance:=eta*integral_abs+eps;

    error:=Abs(table[0]-current_estimate)+Abs(current_estimate-previos_estimate);

    done:=(error<tolerance);

end;

Inc(n);

done:=done or(n>max);

previous_estimate:=current_estimate;

current_estimate:=table[0];

r:=r+r;

until done;

     romberg:=current_estimate;

end;