Различные методы вычисления определенных интегралов

1 2 3

Содержание

Введение 2

1. Различные методы вычисления определенных интегралов 3

1.1. Метод Симпсона для интегрирования функций F (x) по

заданному промежутку и его реализация на языке Pascal 4

1.2. Метод Симпсона для интегрирования функции от двух

переменных F (x, y) по прямоугольной двумерной области и его

реализация на языке Pascal 5

1.3. Метод Ромберга и его реализация на языке Pascal 7

1.4. Метод Гаусса и его реализация на языке Pascal 10

Заключение 16

Литература 17

Введение

Система программирования Турбо Паскаль представляет собой единство двух в известной степени самостоятельных начал: компилятора с языка программирования Паскаль (язык назван в честь выдающегося французского математика и философа Блеза Паскаля (1623-1662)) и некоторой инструментальной программной оболочки, способствующей повышению эффективности создания программ.

Паскаль – гибкий и развитый в отношении типов данных язык. Привлекательны его рекурсивные возможности, а также поддержка технологии объектно-ориентированного программирования.

Изучение программирования на языке Паскаль может дать хороший старт в огромный и увлекательный мир программирования. Обучение языку программирования проходит намного более эффективно с изучением примеров.

В данной работе рассмотрен пример использования языка программирования высокого уровня Pascal для вычисления определенных интегралов.

Различные методы вычисления определенных интегралов.

Приближенное вычисление интеграла,

I = ,

Основано на его замене конечной суммой:

I _n = _kF (x_k),

где w_k – числовые коэффициенты, а x_k – точки отрезка [ x ₀, x ₁]. Приближенное равенство

I ≈ I _n называется квадратурной формулой, точки x_k – узлами квадратурной формулы, а числа w_k – коэффициентами квадратурной формулы. Разные методы приближенного интегрирования отличаются выбором узлов коэффициентов. От этого выбора зависит погрешность квадратурной формулы.

R _n =‌ ‌.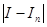

В модуле integral реализовано несколько методов численного интегрирования как для простых (одномерных), так и для кратных (многомерных) интегралов.

В функции simpson реализован стандартный метод Симпсона для интегрирования функции F (x) по заданному промежутку, когда число разбиений интервала выбирается заранее. Функция double_simpson является прямым обобщением метода Симпсона на случай интегрирования функции от двух переменных F (x, y) по прямоугольной двумерной области.

Функция adaptive_simpson служит для вычисления простых интегралов, она корректирует число и размер разбиений интервала, чтобы ошибка вычисления интеграла попала в заранее заданный интервал. Этот метод называется адаптивным интегрированием. Все современные программы интегрирования так или иначе адаптивны.

В функции romberg запрограммирован еще один метод адаптивного интегрирования – метод Ромберга, в настоящее время, вероятно, один из наиболее популярных. Имеются также функция gauss – одномерная версия метода интегрирования Гаусса. Интерфейсная секция модуля integral приведена в листинге 1.1.

Листинг 1. 1. Интерфейсная секция модуля integral.

Unit integral;

Interface

Const

Max_dim =10;

Max_deg=96;

Type

Real_fun=function(x:real):real;

Real_fun2=function(x,y:real):real;

Real_vec=array[1..max_dim+1] of real;

Index=array[1..max_dim+1] of word;

Vec_fun=function(j:word; x:real_vec):real;

Var

no_evaluations, highest_level:word;

function simpson(F:real_fun; x0,x1:real; div_no:word):real;

function double_simpson(F:real_fun2; x0,x1,y0,y1:real; x_div,y_div:word):real;

function adaptive_simpson(F:real_fun;x0,x1,eps,eta:real):real;

function romberg(f:real_fun; x0,x1,eps,eta:real; min,max:word):real;

function gauss3(F:real_fun;x0,x1:real; n:word):real;

procedure compute_gauss_coeffs(deg:word);

function gauss(Freal_fun:x0,x1:real; deg:word):real;

1.1. Метод Симпсона для интегрирования функций F (x) по заданному промежутку и его реализация на языке Pascal.

Перейдем к секции реализации. Она начинается описанием функции simpson. Стоит сказать несколько слов о выборе узлов и коэффициентов квадратурной формулы Симпсона. Идея трехточечного метода Симпсона заключается в следующем.

Пусть x _m – это средняя точка интервала [ x ₀, x ₁] и пусть Q (x) – единственный полином второй степени, который интерполирует (приближает) подынтегральную функцию F (x) по точкам x ₀, x _m и x ₁. Искомый интеграл аппроксимируется интегралом от функции Q (x):

I≈ .

Это оценка точна, если F (x) является полиномом степени 3.

В функции simpson интервал интегрирования делится на div_no равных частей, а трехточечная формула Симпсона применяется к каждому такому интервалу. Параметрами функции simpson (листинг1.2) являются, по порядку, подынтегральная функция, нижняя и верхняя границы интервала интегрирования и количество подынтервалов.

Листинг 1.2. Функция simpson модуля integral

Implementation

Uses crt;

Var

zero, weight:array [1..max_deg] of real;

Function simpson(F:real_fun; x0,x1:real; div_no:word):real;

Var

x, dx, sum:real;

j:word;

begin

dx:=(x1-x0)/(2.0*div_no);

sum:=F(x0)+F(x1);

x:=x0;

for j:=1 to 2*div_no-1 do

begin

x:=x+dx;

if Odd (j) then

sum:=sum+4.0*F(x)

else

sum:=sum+2.0*F(x);

end;

simpson:=dx*sum/3.0;

end;

1.2. Метод Симпсона для интегрирования функции от двух переменных F (x, y) по прямоугольной двумерной области и его реализация на языке Pascal.

Функция double_simpson (листинг 1.3.) является, по существу, прямым обобщением одномерного метода Симпсона на случай вычисления двойного интеграла по прямоугольной области.

Листинг 1.3. Функции double_simpson и simple_simpson модуля integral

Function double_simpson(F:real_fun2; x0,x1,y0,y1:real; x_div,y_div:word):real;

var

dx,dy,x,sum:real;

i:word;

function simple_simpson(x:real):real;

var

y,sum:real;

j,v:word;

begin

sum:=F(x,y0)+F(x,y1);

y:=y0;

for j:=1 to 2*y_div-1 do

begin

y:=y+dy;

if Odd(j) then

sum:=sum+4.0*F(x,y)

else

sum:=sum+2.0*F(x,y);

end;

simple_simpson:=sum;

end;{simple_simpson}

begin{doudle_simpson}

dx:=(x1-x0)/(2.0*x_div);

dy:=(y1-y0)/(2.0*y_div);

x:=x0;

sum:=simple_simpson(x0)+simple_simpon(x1);

for i:=1 to 2*x_div-1 do

begin

x:=x+dx;

if Odd(i) then

sum:=sum+4.0*simple_simpson(x)

else

sum:=sum+2.0*simple_simpson(x);

end;

double_simpson:=dx+dy*sum/9.0;

end;{double_simpson}

Недостатком рассмотренных функций интегрирования является то, что они не дают возможности явно задать точность вычисления интеграла. Точность связана с количеством точек разбиения, но ее значение в этих функциях не определяется с адаптивным выбором шага разбиения. Такой функцией является adaptive_simpson. Параметры eps и eta задают соответственно абсолютную и относительную погрешности. Их роль поясняется следующим неравенством:

Функция adaptive_simpson (листинг1.4) использует рекурсивную процедуру simpson3point, которая вычисляет значение интеграла по интервалу [ x ₀, x ₀+ δx ], где x₀ – не обязательно исходная левая граничная точка.

Если трехточечный метод Симпсона не дает достаточную точность на данном интервале, этот интервал делится на три равные части, и метод вновь применяется к каждой из полученных частей. В результате получим 7 точек разбиения, но вычислять функцию F (x) придется только в четырех из них, поскольку значения в других трех точках уже известны.

При адаптивном разбиении имеется одна тонкость. При переходе к подынтервалам, составляющим одну треть от исходного, чтобы получить новые абсолютную и относительную погрешности, надо поделить eps и eta на .