2020-01-14
96
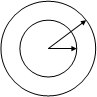
Рассмотрим волоконный световод без потерь двухслойной конструкции, приведенный на рис. 1
|
b
n2 n1 a
Рис. 1 |
Для описания поведения электромагнитного поля в сердечнике (0<r<a) и в оболочке (a<r<b) необходимо использовать различные функции. Исходя из физической сущности процессов, функции внутри сердечника при r=0 должны быть конечными, а в оболочке описывать спадающее поле.
Для определения основных параметров световодов (критической частоты, волнового числа, скорости передачи и др.) воспользуемся основными уравнениями электродинамики – уравнениями Максвелла, которые для диэлектрических волноводов имеют вид:
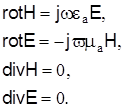(1)
Уравнения Максвелла справедливы для любой системы координат. Для направляющих систем эти уравнения наиболее часто применяются в цилиндрической системе координат, ось Z которой совместим с оптической осью световода:
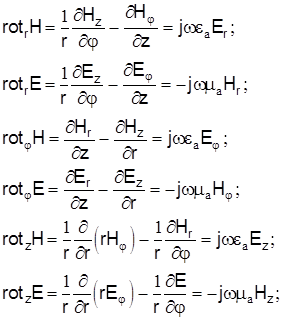(2)
Для решения инженерных задач электродинамики необходимо знать продольные составляющие полей Еz и Hz. Их можно получить следующим образом. Преобразуем первое из уравнений Максвелла (1) к виду
|
|
|
.
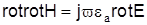Тогда, используя соотношение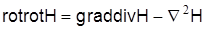 
, а также учитывая, что divH=0, получим
,
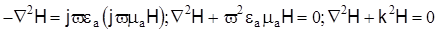где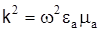 
- волновое число световода.
Поступая аналогично со вторым уравнением Максвелла (2), получим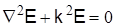 
.
Отсюда следует, что продольные электромагнитные составляющие векторов Ez и Hz удовлетворяют уравнениям
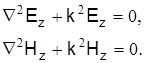
Где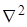 
– оператор Лапласа.
,
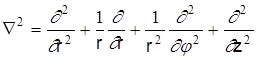Тогда для продольных составляющих Ez и Hz в цилиндричееской системе координат получим дифференциальные уравнения второго порядка:
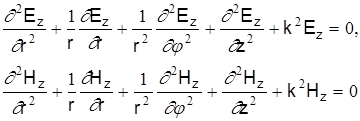(3)
Допустим, что напряженность электромагнитного поля в направлении оси Z меняется по экспоненциальному закону, т.е.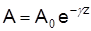 
, где А – любая составляющая векторов Е или Н; 
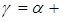j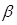 
- коэффициент распространения. Тогда первая и вторая производные определятся
.
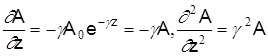Для составляющей Еz
.
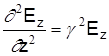Подставляя полученное значениe в уравнения (3), получим
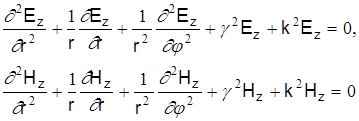
Введем обозначение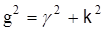 
– поперечное волновое число световода. Тогда для сердечника световода имеем
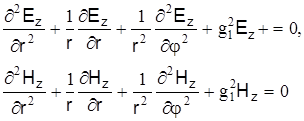(4)
где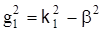 
(без учета затухания) – поперечное волновое число сердечника; k1 – волновое число сердечника с коэффициентом преломления n1, 
.
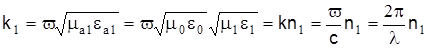Решение уравнений (4) для сердечника следует выразить через цилиндрические функции первого рода – функции Бесселя, имеющие конечные значения при r=0. Поэтому можно написать
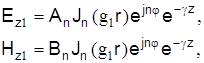(5)
где Аn и Вn – постоянные интегрирования.
Воспользовавшись уравнениями (2), рассмотрим связь между поперечными и продольными компонентами поля. В частности, для составляющей Еr имеем
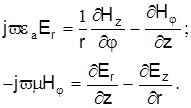
Возьмем производную от второго выражения по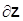 
|
|
|
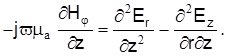
Учитывая, что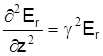 
, а 
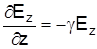, то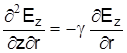 
Тогда
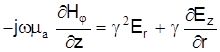или 
Подставим данное выражение в уравнение для Еr
или
.
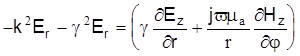Окончательно получим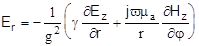 
.
Аналогично можно установить связь между продольными и другими поперечными компонентами поля
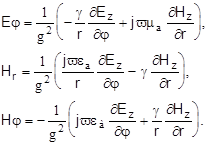
Воспользовавшись уравнениями (5) возьмем соответствующие производные
Тогда выражения для поперечных составляющих электрического и магнитного полей в сердечнике световода, полагая, что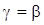 
, имеют вид (множитель 
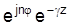не пишем):
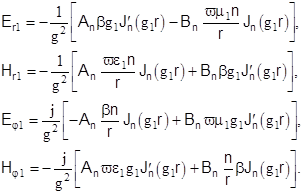(6)
Для оболочки имеем аналогичную систему уравнений:
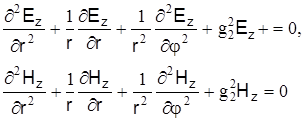
где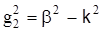 
(без учета затухания) – поперечное волновое число оболочки световода; k2 – волновое число оболочки с коэффициентом преломления n2, 
.
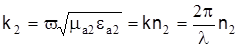Для решения данных уравнений, исходя из условия, что при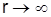 
поле должно стремиться к нулю, следует использовать цилиндрические функции третьего рода – функции Ганкеля:
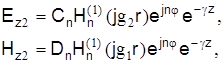
где Сn, Dn – постоянные интегрирования.
Тогда для поперечных составляющих поля в оболочке можно написать следующие выражения:
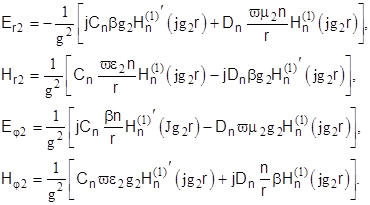(7)
Постоянные интегрирования Аn, Вn, Сn, Dn могут быть определены на основании граничных условий. Используем условия равенства тангенциальных составляющих напряженностей электрических и магнитных полей на поверхности раздела сердечник-оболочка (при r=а):
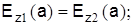
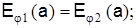
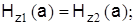
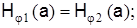
Найдя постоянные интегрирования и подставив их в уравнения, после соответствующих преобразований получим следующее трансцендентное уравнение:
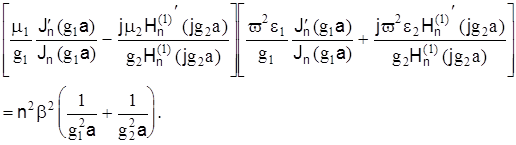(8)
Полученные уравнения дают возможность определить неизвестные постоянные и найти структуру поля в сердечнике и оболочке волоконного световода. В общем случае уравнения имеют ряд решений, каждому из которых соответствует определенная структура поля, называемая типом волны или модой.
световод уравнение интегрирование волна
