Основные этапы решения нелинейных уравнений

ВВЕДЕНИЕ

В данной работе необходимо рассмотреть решение систем нелинейных уравнений методом Ньютона.

Данный метод был описан Исааком Ньютоном в рукописи «Об анализе уравнениями бесконечных рядов», адресованной в 1669 году английскому математику Исааку Барроу, и в работе «Метод флюксий и бесконечные ряды» или «Аналитическая геометрия». В своих работах Ньютон вводит такие понятия, как разложение функции в ряд, бесконечно малые и флюксии (производные в нынешнем понимании). Указанные работы были изданы значительно позднее: первая вышла в свет в 1711 году благодаря Уильяму Джонсону, вторая была издана Джоном Кользоном в 1736 году уже после смерти создателя. Однако описание метода существенно отличалось от его нынешнего изложения: Ньютон применял свой метод исключительно к полиномам. Он вычислял не последовательные приближения , а последовательность полиномов и в результате получал приближённое решение .

ОСНОВНЫЕ ЭТАПЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.

Нелинейным уравнением называется уравнение вида

, (1.1)

где - нелинейная функция вида:

- нелинейная алгебраическая функция (полином или многочлен);

- тригонометрическая, логарифмическая, показательная функция;

- комбинирование этих функций, например .

Решением нелинейного уравнения (1.1) называется такое значение , которое при подстановке в уравнение (1.1) обращает его в тождество.

На практике не всегда удается найти точное решение. В этом случае решения уравнения (1.1) находят с применением приближенных (численных) методов.

Приближенным решением нелинейного уравнения (1.1) называется такое значение , при подстановке которого в уравнение (1.1) последнее будет выполняться с определенной степенью точности.

Нахождение приближенных решений составляет основу численных методов и вычислительной математики. Решение нелинейных уравнений и их систем распадается на два этапа: отделение корней уравнений и уточнение корней нелинейных уравнений.

На первом этапе необходимо исследовать уравнение и выяснить, имеются корни или нет. Если корни имеются, то необходимо определить их количество и затем найти интервалы, в каждом из которых находится только один корень, т.е. отделить корни.

Первый способ отделения корней – графический. Данный метод позволяет определить количество корней на отрезке, но не единственность корня. Если имеет простой аналитический вид, то, исходя из уравнения (1.1), можно построить график функции . Тогда точки пересечения графика функции с осью абсцисс будут являться приближенными значениями корней исходного нелинейного уравнения. Если имеет сложный аналитический вид, то можно представить её в виде разности двух более простых функций . Так как , то выполняется равенство . После построения графиков и задача решения нелинейного уравнения сводится к поиску абсцисс точек пересечения двух графиков, которые и будут являться приближенными значениями корней уравнения (1.1).

Второй способ отделения корней – аналитический. Процесс отделения корней здесь основывается на следующих теоремах:

1) если функция непрерывна на отрезке и на концах отрезка принимает значения разных знаков (т.е. ), то на содержится хотя бы один корень.

2) если функция непрерывна на отрезке , выполняется условие вида и производная сохраняет знак на , то на отрезке имеется единственный корень.

3) если функция является многочленом n -й степени и на концах отрезка принимает значения разных знаков, то на имеется нечетное количество корней. Если на концах отрезка функция меняет знак, то уравнение (1.1) либо не имеет корней на , либо имеет четное количество корней.

При аналитическом методе исследований необходимо выявить интервалы монотонности функции . Для этого необходимо найти критические точки , т.е. точки, в которых первая производная равна нулю или не существует. Тогда вся числовая ось разбивается на интервалы монотонности , на каждом из которых определяется знак производной , где . Затем выделяются те интервалы монотонности , на которых функция меняет знак, то есть выполняется неравенство 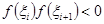. На каждом из этих интервалов для поиска корня используются методы уточнения корней.