Биномиальное распределение

Биномиальное распределение в теории вероятностей — распределение количества «успехов» в последовательности из n независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна p.

Пусть 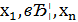— конечная последовательность независимых случайных величин с распределением Бернулли, то есть

Построим случайную величину Y:

. .

Тогда Y, число единиц (успехов) в последовательности , имеет биномиальное распределение с n степенями свободы и вероятностью «успеха» p. Пишем:  . Её функция плотности вероятности задаётся формулой:

где — биномиальный коэффициент.

Функция распределения биномиального распределения может быть записана в виде суммы:

,

где обозначает наибольшее целое, не превосходящее число y, или в виде неполной бета-функции: .

Производящая функция моментов биномиального распределения имеет вид:

,

откуда

,

,

а дисперсия случайной величины.

.

Свойства биномиального распределения

Пусть  и  . Тогда  .

Пусть  и  . Тогда .

Связь с другими распределениями:

Если n = 1, то, очевидно, получаем распределение Бернулли.

Если n большое, то в силу центральной предельной теоремы , где N(np,npq) — нормальное распределение с математическим ожиданием np и дисперсией npq.

Если n большое, а λ — фиксированное число, то  , где P(λ) — распределение Пуассона с параметром λ.

 

 

Закон Пуассона

Второй предел биноминального распределения, представляющий практический интерес, относится к случаю, когда при неограниченном увеличении числа испытаний математическое ожидание остается постоянным:

Если при , , то перейдя к противоположному событию, мы получим тот же случай. Полагая m << n, получим при

 

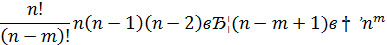
Следовательно,

Полученное распределение вероятностей случайной величины называется законом Пуассона.

Распределение Пуассона имеет максимум вблизи
(знак [x] обозначает целую часть числа x, меньшую или равную x).

Числовые характеристики распределения:
Математическое ожидание
Дисперсия

Распределение Пуассона играет важную роль для описания "редких" событий в физике, теории связи, теории надежности, теории массового обслуживания и т.д. – там, где в течение определенного времени может происходить случайное число каких-то событий (радиоактивных распадов, телефонных вызовов, отказов оборудования, несчастных случаев и т.п.).