Проверочный силовой расчёт выходной зубчатой передачи

 

Сделаем проверочный силовой расчёт на выносливость выходной зубчатой передачи по изгибной усталости.

Условие прочности:

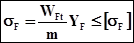, (3.1)

где 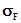- напряжение при изгибе;

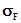  [ ] - предельно допустимое напряжение при изгибе, определяемое по формуле:

для колеса: 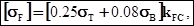    (3.2.1),

 

для шестерни: 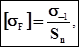                                        (3.2.2);

где s_T- предел текучести материала (в Н/мм²);

s_B - предел прочности материала (в Н/мм²);

   s_-1 – предел выносливости материала, определяемый по формуле:

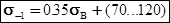, (3.2.3)

   S_n  - запас прочности;

  k_FC = 0.8 - коэффициент, учитывающий влияние реверсивности передачи;

m - модуль зубчатого колеса;

Y_F - коэффициент, учитывающий влияние формы зуба;

W_Ft - удельная, нагрузка по ширине зуба, определяемая по формуле:

 

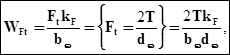(3.3)

 

где T – крутящий момент, действующий на зубчатое колесо;

     k_F - коэффициент, учитывающий влияние неравномерности распределения нагрузки;

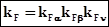 , (3.4)

 

где 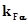- коэффициент, учитывающий влияние неравномерности распределения нагрузки между зубьями;

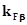- коэффициент, учитывающий влияние неравномерности распределения нагрузки по ширине зуба;

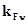- коэффициент, учитывающий влияние динамической нагрузки;

b_w - рабочая ширина венца зубчатой передачи;

d_w=d - диаметр делительной окружности зубчатого колеса.

 

1). Проведём расчёт на выносливость колеса.

Материал колеса: Бр. ОЦ 4-3т

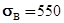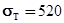Мпа;

Мпа;

По формуле (3.2.1) определяем:

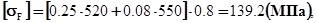
По [3]: 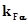                  =1; 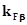     =1.02;

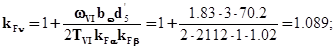
По формуле (3.4) определяем :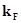

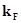=1×1.02×1.089=1.11

По формуле (3.3) определяем :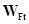

;

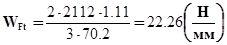По [3]: 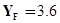       для z = 117;

По формуле (3.1) определяем :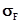

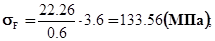
133.56 < 139.2 т.е. < ;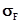

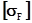Условие прочности выполняется.

 

2). Проведём расчёт на выносливость шестерни.

Материал шестерни: Сталь 40ХН, обработка - улучшение

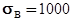МПа;

     S_n = 1.1

По формуле (3.2.3) определяем:

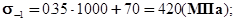
По формуле (3.2.2) определяем:

 

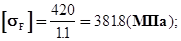
По [3]: 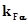                  =1; 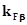     =1.02;

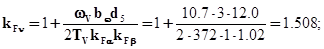
По формуле (3.4) определяем :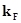

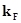=1×1.02×1.508=1.538;

По формуле (3.3) определяем :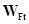

;

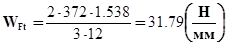По [3]: 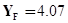       для z = 20;

По формуле (3.1) определяем :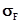

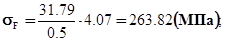
258.77 < 381.8 т.е. < ;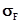

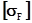Условие прочности выполняется.