Правило парамодуляции

Если для заданных предложений C1 и C2 = (a’ = b’, B) ( или C2’ = (b’ = a’, B)), не имеющих общих переменных в общей части B выполняются условия:

1. C1 содержит терм d.

2. У d и a’ есть наиболее общий унификатор:

,

 

где ui и wj – переменные соответственно из a’ и d,

то надо построить предложения = C1p1, а затем C#, заменяя a’ на b’p2 для какого-то одного вхождения a’ в C₁^*. Наконец вывести:

C3=(C#, Bp).

 

Формулировка весьма сложна, но ее реализация очень проста. В простейшем случае B пусто, так что предложения, содержащие высказывания с равенством, состоят из единственного атома выражающего равенство. Таким образом, из:

C1={Q(a)},

C2={a=b}

 

можно вывести:

C3={Q(b)}.

 

Несколько более сложный случай:

C1={Q(x)},

C2={(a=b)}.

 

Подстановка p = (a/x) дает:

C1^*={Q(a)},

C3={Q(b)}.

 

При одном применении парамодуляции подстановка a=bp2 применяется в С₁^* только один раз. Таким образом, если заданы предложения:

C1={Q(x), P(x)},

C2={(a=b)},

 

то одно применение парамодуляции с подстановкой p = (a/x) дает сначала

C₁^*={Q(a), P(a)},

 

а затем или

C3={Q(a),P(b)},

 

либо

C3={Q(b), P(a)}.

 

Для получения C4={Q(b), P(b)} требуется повторное применение парамодуляции.

Рассмотрим пример по сюжету известной сказки Андерсона «Принцесса на горошине», который может служить тестом на наличие королевской крови.

Определения для примера:

1. x, y, z – переменные, принимающие значения на множестве людей.

2. M(x): x – мужчина.

3. C(x): x – простолюдин.

4. D(x): x может почувствовать горошину через перину.

5. x = k: x – король.

6. x = q: x – королева.

7. d(x,y): дочь x и y.

8. x = p: x – принцесса.

Исходные предложения:

 - существует мужчина.

 - существует женщина.

 - любой мужчина не простолюдин король.

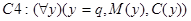 - любая королева – женщина и не простолюдинка.

 - дочь короля и королевы – принцесса.

 - принцесса может почувствовать горошину.

Удалим квантор существования из предложений C1, C2, обозначив через f1, f2 сколемовские функции без переменных, так как перед квантором существования нет квантора общности.

 : f1 – мужчина.

  f2 – женщина.

Опускаем кванторы всеобщности в C3, C4. Проводим резолюцию C1 с C3, а затем C2 и C4. Получаем:

  f1 – король или простолюдин.

  f2 – королева или простолюдинка.

Затем осуществляем парамодуляцию C7 и C5. Это дает:

 дочь королевы и f1 – есть принцесса или f1 - простолюдин. Затем осуществляем парамодуляцию C8 и C9. Это дает:

 дочь f1 и f2 есть принцесса, либо f1, либо f2 – простолюдин. Наконец парамодуляция C10 с C6 дает:

 дочь f1 и f2 может почувствовать горошину, либо f1, либо f2 – простолюдин.

 

4.2.4 Стратегии очищения

Применение принципа резолюции без ограничений может привести к слишком большому количеству предложений, чтобы с ним можно было бы работать на практике. Поэтому надо уметь заранее определять, какие выполнять резолюции и какие производить выводы. На этом и основываются стратегии очищения.

4.2.4.1 Стратегия предпочтения одночленов

В стратегии предпочтения одночленов требуется, чтобы на каждом шаге вывода все резолюции, использующие предложения только с одним литералом, вычислялись прежде других резолюций. В общем случае резолюции, использующие короткие предложения, выполняются перед резолюциями с более длинными предложениями. Эта стратегия скорее относится к упорядочиванию, а не к очищению, так как она меняет лишь порядок выполнения, но ни одну из возможных резолюций не исключает из рассмотрения.

4.2.4.2 Факторизация

Размер предложений по длине можно уменьшить, используя подстановки, так что некоторые литералы в предложении становятся одинаковыми. Эта операция называется факторизацией. Например:

C = {A(x, f(k)), A(b, y), A(a, f(x)), A(x, z)}

 

можно факторизовать подстановкой:

q =(b/x, f(k)/y, f(b)/z).

 

Тогда получим:

Cq = {A(b, f(k)), A(a, f(b)), A(b, f(b))}.

Cq называется факториалом предложения C. Фактор предложения не обязательно единственный. Другой фактор:

p = (a/x, f(k)/y, f(a)/z),

Cp = {A(a, f(k)), A(b, f(k)), A(a, f(a)}.

4.2.4.3 Использование подслучаев

Для любой пары предложений C, D Î S предложение C называется подслучаем предложения D, если существует такая подстановка p, что Cp Í D. Например:

C = {A(x)},

D = {A(b), P(x)},

 

то подстановка

p = (b/x)

 

приведет к

Cp = {A(b)}.

 

то означает сокращение литералов.

 

4.2.4.4 Гиперрезолюция

Можно делать так, чтобы в резолюции участвовали сразу по несколько предложений. Это называется гиперрезолюцией. Предположим, что для конечного множества предложений {C1, …, Cn} и единственного предложения B удовлетворяются следующие условия:

1. B содержит n литералов L1, …, Ln.

2. Для каждого i, 1£ i £ n, предложение Ci, содержит литерал , но не содержит дополнений никакого другого литерала из B и никакого литерала из любого предложения Cj, j ¹ i.

Множество Sa = {Ci} È {B} будем называть конфликтом, а предложение:

 

 

его гиперрезольвентой. Ra можно вывести из Sa.

В большинстве случаев к конфликту приходят после соответствующих подстановок. Иными словами, для заданного множества предложений Sa, не удовлетворяющего определению конфликта, может найтись такая подстановка p, что Sap будет конфликтом. Тогда Sa называется скрытым конфликтом.

В качестве примера гиперрезолюции рассмотрим множества:

 

 

Подстановка p =(a/x, b/y) дает

 

Sap - конфликт с резольвентой , и Sa – скрытый конфликт.

4.2.4.5С – упорядочение

С – упорядочение предполагает линейность, так как при его определении различаются левое и правое родительские предложения. Пусть С – предложение из S. Обозначим через [C] предложение C с заданным на нем произвольным порядком литералов, а через [S] – множество таких упорядоченных предложений. Если предложение [C] порождается в линейном выводе  то пусть [C^i-1] и [B^i-1] будут его левым и правым предложениями с литералами предложения C^i-1, расположенными в порядке  (где  т.е. самый правый литерал левого родительского выражения является литералом резолюции), и с литералами предложения B^i-1 в порядке . Ясно, что для  некоторого i (i =1¸m). Тогда упорядоченное предложение Cⁱ таково:

 

 

т.е. литералы правого родительского предложения добавляются к литералам левого, при этом литералы резолюции, естественно, опускаются, а в случае повторения литералов сохраняются те, что расположены слева. Резолюция допускается только с самым правым литералом предложения Cⁱ.

Пример: