Обобщение понятия степени

Определение: Пусть , корнем -ой степени из чиста  называется такое число, -я степень которого равна .

Согласно данному определению корень -ой степени из числа  – это решение уравнения . Число корней этого уравнения зависит от 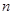 и . Рассмотрим функцию . Как известно, на промежутке  эта функция при любом 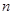   возрастает и принимает все значения из промежутка . По теореме о корне уравнение  для любого  имеет неотрицательный корень и при том только один. 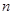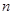Его называют арифметическим корнем -ой степени из числа  и обозначают ; число  называют показателем корня, а само число  – подкоренным выражением. Знак  называют так же радикалом.

Определение: Арифметическим корнем 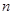-ой степени из числа  называют неотрицательное число, 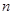-я степень которого равна .

При четных 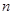 функция  четна. Отсюда следует, что если , то уравнение , кроме корня , имеет также корень . Если , то корень один: ; если , то это уравнение корней не имеет, поскольку четная степень любого числа неотрицательна.

При нечетных значениях 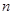 функция  возрастает на всей числовой прямой; её область значений – множество всех действительных чисел. Применяя теорему о корне, находим, что уравнение  имеет один корень при любом  и, в частности, при . Этот корень для любого значения  обозначают .

Для корней нечетной степени справедливо равенство . В самом деле, , т.е. число –  есть корень 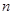-й степени из . Но такой корень при нечетном 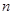 единственный. Следовательно, .

Замечание 1.   Для любого действительного

Замечание 2.   Удобно считать, что корень первой степени из числа  равен . Корень второй степени из числа  называют квадратным корнем, а корень третьей степени называют кубическим корнем.

Напомним известные свойства арифметических корней -ой степени.

Для любого натурального 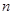, целого  и любых неотрицательных целых чисел  и  справедливы равенства:

                 1. .

                 2. .

                3. .

    4.

    5. .

Перейдём к введению степени с рациональным показателем.

Выражение  определено для всех  и , , кроме случая  при . Напомним свойства таких степеней.

    Для любых чисел ,  и любых целых чисел  и  справедливы равенства:               

Отметим так же, что если , то  при  и  при       

Определение: Степенью числа  с рациональным показателем , где 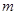 – целое число, а  – натуральное , называется число .

Итак, по определению .

При сформулированном определении степени с рациональным показателем сохраняются основные свойства степеней, верные для любых показателей (разница заключается в том, что свойства верны только для положительных оснований).