Определение: Логарифмом числа  по основанию
по основанию 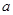 называется показатель степени, в которую нужно возвести основание
называется показатель степени, в которую нужно возвести основание 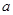 , то бы получить число
, то бы получить число  .
.
Формулу  (где
(где  ,
, 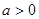 и
и  ) называют основным логарифмическим тождеством.
) называют основным логарифмическим тождеством.
При работе с логарифмами применяются следующие их свойства, вытекающие из свойств показательной функции:
При любом 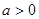 (
( ) и любых положительных
) и любых положительных  и
и  выполнены равенства:
выполнены равенства:
1. 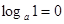
2. 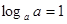
3. 
4. 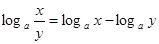
5.  для любого действительного
для любого действительного  .
.
Основные свойства логарифмов широко применяются в ходе преобразования выражений, содержащих логарифмы. Например, часто используется формула перехода от одного основания логарифма к другому:  .
.
Перейдём к определению логарифмической функции
Пусть 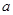 – положительное число, не равное 1.
– положительное число, не равное 1.
Это функция вида 
ü Число 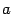 называется основанием логарифма. Обратим внимание читателя на то, что с точностью до поворотов и симметричных отражений на последних четырёх чертежах изображена одна и та же линия. Область определения логарифмической функции – промежуток (0; +¥).
называется основанием логарифма. Обратим внимание читателя на то, что с точностью до поворотов и симметричных отражений на последних четырёх чертежах изображена одна и та же линия. Область определения логарифмической функции – промежуток (0; +¥).
ü Область значения логарифмической функции – вся числовая прчмая.
ü Логарифмическая функция непрерывна и дифференцируема во всей области определения. Производная логарифмической функции вычисляется по формуле
(loga x)¢ =
ü Логарифмическая функция монотонно возрастает, если а >1. При 0< a <1
ü Логарифмическая функция с основанием а монотонно убывает.
ü При любом основании a >0, a ¹1, имеют место равенства
loga 1 = 0, loga a =1.
ü При а >1 график логарифмической функции – кривая, направленная вогнутостью вниз; при 0< a <1 – кривая, направленная вогнутостью вверх.
при  график имеет такой вид:
график имеет такой вид:

При  график получается такой:
график получается такой:

Глава 3.
Тождественные преобразования показательных и
Логарифмических выражений на практике.
Задание 1.
Вычислите:
1)  ;
;
2) 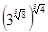 ;
;
3)  ;
;
4) 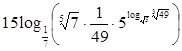 ;
;
5) 
Решение:
1) Используя свойство степени, получим:

 ;
;
Ответ: 27
2) 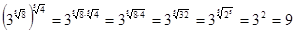 ;
;
Ответ: 9
2) Применяя свойства логарифмов и степени:
3) 
 ;
;
Ответ: 24
4) 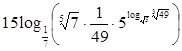
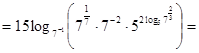
 ;
;
Ответ: 7
5) Известно, что  =1, а
=1, а  =0, поэтому:
=0, поэтому:



 . Ответ: 0
. Ответ: 0
Задание 2.
Упростите выражения:
1)  ;
;
2)  ;
;
3)  .
.
Решение:
Применим свойства степени:
1) 
 ;
;
Ответ: 
2) Откроем скобки и приведём подобные слагаемые:

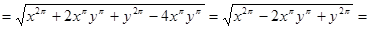
 , т.к.
, т.к. 
Ответ: 
3) Воспользуемся формулами перехода к новому основанию




Ответ: 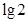
Задание 3.
Найдите значение выражений:
1)  ;
;
2)  ;
;
3)  ;
;
4) 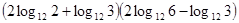 .
.
Решение:
1) Воспользуемся свойствами логарифмов


Ответ: 2
2) 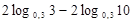

Ответ: 2
3) 

Ответ: -3
4) 


Ответ: 1
Задание 4.
Прологарифмируйте по основанию  выражение:
выражение:
1)  при
при  ;
;
2)  при
при  ,
,  ,
, 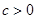 .
.
Решение:
1) Согласно свойствам логарифма:


Ответ: 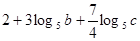
2) 

Ответ:  .
.
Задание 5.
Найдите  , если:
, если:
1)  ;
;
2)  .
.
Решение:
1) Применяя свойства логарифмов:



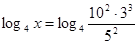
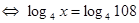

Ответ: 108
2) 


 .
.
Ответ:  .
.
Задание 6.
Известно, что 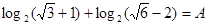 . Найти
. Найти  .
.
Решение:
Домножим и разделим выражения, стоящие под знаком логарифма на сопряженные:



 .
.
Ответ:  .
.
Задание 7.
Решите уравнения:
1)  ;
;
2)  ;
;
3)  .
.
Решение:
1) Перейдём к основанию 2 в обеих частях уравнения



Ответ: -2; 4
2) Число 2,25 запишем в виде обыкновенной дроби





 , так как
, так как  , то
, то  , получаем, что
, получаем, что 
Ответ: 0,25
4) Применим свойства логарифмов


 .
.
Ответ:  .
.
Заключение
В данной курсовой работе по теме «Тождественные преобразования показательных и логарифмических выражений» мною было рассмотрено введение данного материала в обучение в школьном курсе алгебры и начала анализа.
Тема тождественных преобразований, в общем, является одной из часто используемых в вычислениях и решении различных задач. Поэтому о преобразованиях начинают говорить уже с начала средней школы при изучении математики.
В работе были приведены задания, разные по сложности и по содержанию, с использованием тождественных преобразований. Данные задания могут быть использованы для проведения контрольных или самостоятельных работ проверки знаний учащихся.
Список использованной литературы:
1. «Математический анализ» Н.Я. Виленкин, С.И. Шварцбурд
Изд. «просвещение», М.:1969 г.
2. Ильин «Основы Математического анализа», М.: 2004 г.
3. Алгебра и начала анализа. Под ред. Колмогорова А.Н. М.: Просвещение, 1991г.
4. И.Ф. Шарыгин, В.И. Голубев. Факультативный курс по математике (решение задач). Уч.пособие для 11 кл. М.: Просвещение, 1991г.
5. Зорич В.А. «Математический анализ» для студентов физ.-мат. Факультетов, М.: 2007 г.
6. Черкасов Р.С., Столяр А.А. Методика преподавания математики в средней школе. М.: Просвещение, 1985г.
7. Учебник «Алгебра и начала анализа 10-11» под редакцией А.Н. Колмогорова
8. «Дидактические материалы по алгебре и началам анализа для 11 класса» Б.М. Ивлев, С.М. Саакян, С.И. Шварцбург.
 2020-01-14
2020-01-14 145
145







