Показательная функция

Это функция вида (, ). Для неё , ,  ,  и при график имеет такой вид:

При вид графика такой:

1. Число 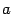 называется основанием показательной функции. Область определения функции – вся числовая прямая.

2. Область значения функции – множество всех положительных чисел.

3. Функция непрерывна и дифференцируема во всей области определения. Производная показательной функции вычисляется по формуле

(a ^x)¢ = a ^xln a

4. При а >1 функция монотонно возрастает, при а <1 монотонно убывает.

5. Показательная функция имеет обратную функцию, называемую логарифмической функцией.

6. График любой показательной функции пересекает ось 0y в точке y =1.

7. График показательной функции – кривая, направленная вогнутостью вверх.

8. При любых действительных значениях  и  справедливы равенства          

Эти формулы называют основными свойствами степеней.

   Можно так же заметить, что функция  непрерывна на множестве действительных чисел.