About application of mathematics in linguistics

1 2 3 4 5 6 7

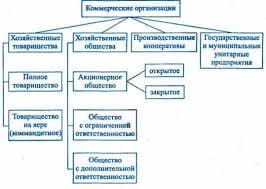
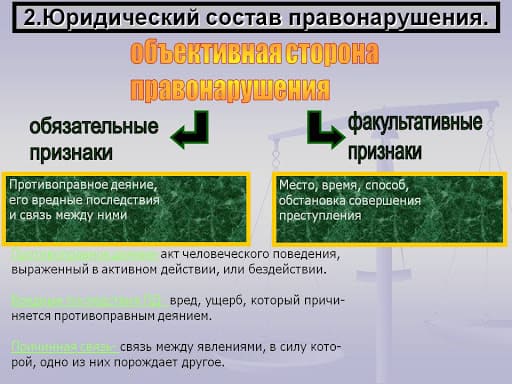
A teacher of English was ill and a teacher of mathematics replaced him.

He began to compose a table of irregular verbs:

Then he said:

- Okay, I mark this form as x. Then it’s possible to compose the proportion:

Unit II.

Prime numbers

Text 1

Prime numbers

Prime numbers and their properties were first studied extensively by the ancient Greek mathematicians. The mathematicians of Pythagoras's school (500 BC to 300 BC) were interested in numbers for their mystical and numerological properties. They understood the idea of primality and were interested in perfect and amicable numbers. A perfect number is one whose proper divisors sum to the number itself. e.g. The number 6 has proper divisors 1, 2 and 3 and 1 + 2 + 3 = 6, 28 has divisors 1, 2, 4, 7 and 14 and 1 + 2 + 4 + 7 + 14 = 28. A pair of amicable numbers is a pair like 220 and 284 such that the proper divisors of one number sum to the other.
In Book of the Elements, Euclid proves that there are infinitely many prime numbers. This is one of the first proofs known which uses the method of contradiction to establish a result. Euclid also gives a proof of the Fundamental Theorem of Arithmetic: Every integer can be written as a product of primes in an essentially unique way. Euclid also showed that if the number 2 ⁿ - 1 is prime then the number 2 ⁿ ^-1(2 ⁿ - 1) is a perfect number. The mathematician Euler (much later in 1747) was able to show that all even perfect numbers are of this form. It is not known to this day whether there are any odd perfect numbers.

There is then a long gap in the history of prime numbers during what is usually called the Dark Ages. The next important developments were made by Fermat at the beginning of the 17^th Century. He proved a speculation of Albert Girard that every prime number of the form 4 n + 1 can be written in a unique way as the sum of two squares and was able to show how any number could be written as a sum of four squares. He devised a new method of factorizing large numbers which he demonstrated by factorizing the number 2027651281 = 44021 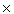46061. He proved what has come to be known as Fermat's Little Theorem (to distinguish it from his so-called Last Theorem). This states that if p is a prime then for any integer a we have a^p = a modulo p.
This proves one half of what has been called the Chinese hypothesis which dates from about 2000 years earlier, that an integer n is prime if and only if the number 2 ⁿ - 2 is divisible by n. The other half of this is false, since, for example, 2³⁴¹ - 2 is divisible by 341 even though 341 = 31 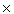11 is composite. Fermat's Little Theorem is the basis for many other results in Number Theory and is the basis for methods of checking whether numbers are prime which are still in use on today's electronic computers.

Number of the form 2 ⁿ - 1 attracted attention because it is easy to show that if unless n is prime these number must be composite. These are often called Mersenne numbers M_n because Mersenne studied them. Not all numbers of the form 2 ⁿ - 1 with n prime are prime. For example 2¹¹ - 1 = 2047 = 23 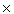89 is composite, though this was first noted as late as 1536. For many years numbers of this form provided the largest known primes. In 1952 the Mersenne numbers M ₅₂₁, M ₆₀₇, M ₁₂₇₉, M ₂₂₀₃ and M ₂₂₈₁ were proved to be prime by Robinson using an early computer and the electronic age had begun. By 2003 a total of 40 Mersenne primes have been found. The largest is M _20996011 which has 6320430 decimal digits.