Понятие задачи линейного программирования

 

Временем рождения линейного программирования принято считать 1939г., когда была напечатана брошюра Л.В. Канторовича «Математические методы организации и планирования производства» [2]. Поскольку методы, изложенные им, были мало пригодны для ручного счета, а быстродействующих вычислительных машин в то время не существовало, работа Л.В. Канторовича осталась почти не замеченной. Свое второе рождение линейное программирование получило в начале пятидесятых годов с появлением ЭВМ. Тогда началось всеобщее увлечение линейным программированием, вызвавшее в свою очередь развитие других разделов математического программирования.

Таким образом, линейное программирование - область математики, разрабатывающая теорию и численные методы решения задач нахождения экстремума (максимума или минимума) линейной (целевой) функции многих переменных при наличии линейных ограничений, т. е. равенств или неравенств, связывающих эти переменные [1].

Задачей линейного программирования называется задача исследования операций, математическая модель которой имеет вид:

 

 

В этом случае говорят, что задача представлена в канонической форме. При этом система линейных уравнений и неравенств, определяющая допустимое множество решений задачи W, называется системой ограничений задачи линейного программирования, а линейная функция f(Х) называется целевой функцией или критерием оптимальности. В частном случае, если I = Ш, то система состоит только из линейных неравенств, а если I = M, то – из линейных уравнений.

Итак, характерные черты задач линейного программирования следующие:

1) показатель оптимальности f(X) представляет собой линейную функцию от элементов решения X = (x ₁, x ₂,..., x_n);

2) ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств.

Любую задачу линейного программирования можно свести к задаче в канонической форме. Для этого в общем случае нужно уметь сводить задачу максимизации к задаче минимизации; переходить от ограничений неравенств к ограничениям равенств и заменять переменные, которые не подчиняются условию неотрицательности. Максимизация некоторой функции эквивалента минимизации той же функции, взятой с противоположным знаком, и наоборот.

Правило приведения задачи линейного программирования к каноническому виду состоит в следующем:

1) если в исходной задаче требуется определить максимум линейной функции, то следует изменить знак и искать минимум этой функции;

2) если в ограничениях правая часть отрицательна, то следует умножить это ограничение на -1;

3) если среди ограничений имеются неравенства, то путем введения дополнительных неотрицательных переменных они преобразуются в равенства;

4) если некоторая переменная x _k не имеет ограничений по знаку, то она заменяется (в целевой функции и во всех ограничениях) разностью между двумя новыми неотрицательными переменными: , где  - свободный индекс, .

При описании реальной ситуации с помощью линейной модели следует проверять наличие у модели таких свойств, как пропорциональность и аддитивность. Пропорциональностьозначает, что вклад каждой переменной в целевой функции и общий объем потребления соответствующих ресурсов должен быть прямо пропорционаленвеличине этой переменной. Аддитивностьозначает, что целевая функция и ограничения должны представлять собой сумму вкладов от различных переменных [4].

Исходя из отмеченных выше особенностей задач линейного программирования, можно наметить следующую общую схему формирования экономико-математической модели:

- выбор некоторого числа переменных величин, заданием числовых значений которых однозначно определяется одно из возможных состояний исследуемого объекта или явления;

- выражение взаимосвязей, присущих исследуемому объекту (явлению), в виде математических соотношений (уравнений, неравенств); эти соотношения образуют систему ограничений задачи;

- количественное выражение выбранного критерия оптимальности в форме целевой функции;

- математическое формулирование задачи как задачи отыскания экстремума целевой функции при условии выполнения ограничений, накладываемых па переменные [1].

Говоря о математических моделях задач линейного программирования, выделяют, как правило, несколько основных видов задач:

- задачи по определению оптимального ассортимента продукции (в качестве критериев оптимальности в них могут быть использованы прибыль, себестоимость, номенклатура производимой продукции и затраты станочного времени);

- задачи по использованию мощностей оборудования (обычно поставлены так, чтобы израсходовать все отведенное время работы машины, т.е. обеспечить полную загрузку машины, при этом количество выпускаемой продукции каждого вида должно быть, по крайней мере, не менее N_j;

- задачи по минимизации дисбаланса на линии сборки (что по существу эквивалентно максимизации выпуска изделий);

- задачи составления кормовой смеси (задача о диете);

- задачи составления жидких смесей (класс моделей, аналогичных рассмотренным выше, возникает при решении экономической проблемы, связанной с изготовлением смесей различных жидкостей с целью получения пользующихся спросом готовых продуктов);

- задачи о раскрое или о минимизации обрезков (состоят в разработке таких технологических планов раскроя, при которых получается необходимый комплекс заготовок, а отходы (по длине, площади, объему, массе или стоимости) сводятся к минимуму);

- транспортные задачи (по распределению ресурсов, находящихся у m производителей (поставщиков), n потребителям этих ресурсов) [3].

Обобщая их, можно сделать следующие выводы.

1. Ограничения в задачах линейного программирования могут быть выражены как равенствами, так и неравенствами.

2. Линейная функция может стремиться как к максимуму, так и к минимуму.

3. Переменные в задачах всегда неотрицательны.

Для решения задач линейного программирования в настоящее время используются несколько основных методов. Среди них:

- графический метод (используемый обычно для решения задач линейного программирования, представленных в стандартном виде, если число переменных в целевой функции и системе ограничений не более двух);

- симплексный метод (стандартный метод решения задач линейного программирования с любым числом переменных, основанный на переходе от одного опорного плана к другому, при котором значение целевой функции улучшается (по крайней мере, не ухудшается);

- решение задач линейного программирования с использованием приложения MS Excel [1].

 

2.2 Построение и решение ЭММ на примере ООО «Дубровчанка+»

 

Пользуясь статистическими данными деятельности предприятия, составим экономико-математическую модель задачи по определению оптимального ассортимента продукции.

 

Наименование изделия	Габаритные размеры, мм	Ед.изм.	Цена, руб.	Усл. обознач.
Кухня "Добровчанка-Н8" (угловая, без раковины, фасад - массив, постформинг)	2400*1600	к-т.	13000-00	A
Шкаф навесной 2-х дверный (фасад - массив)	800*320*720	шт.	1300-00	B
Стол обеденный "Ладога", пластик	110*600*750	шт.	1200-00	C
Кровать подростковая 2-х ярусная	1985*750*1650	шт.	4300-00	F
Комод из массива	800*560*850	шт.	4450-00	G

 

Для производства пяти видов продукции (в таблице) ООО «Дубровчанка +» использует древесину двух видов. Нормы затрат ресурсов на одно изделие каждого вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в следующей таблице:

 

Ресурсы	Нормы затрат ресурсов					Общее кол-во ресурсов
	А	B	C	F	G
Древесина, м3 I Вид	1,5	0,08	0,06	0,2	0,2	350
II Вид	0,2	0,05	0,04	0,2	0,1	130
Трудоемкость, чел. - часы	3,3	0,4	0,3	1	1,2	1100
Прибыль от реализации, тыс. руб.	13000	1300	1200	4300	4450

Определим, сколько единиц каждого изделия следует изготавливать предприятию, чтобы прибыль от их реализации была максимальной.

Решение:

Обозначим изделие каждого вида соответственно a, b, c, f, g. Тогда на изготовление всей продукции уйдет (1,5a+0,08b+0,06c+0,2f+0,2g) м³ древесины I вида и (0,2a+0,05b+0,04c+0,2f+0,1g) м³ древесины II вида. Так как запасы этих ресурсов не превышают 350 и 130 м³ соответственно, то

 

1,5a+0,08b+0,06c+0,2f+0,2g ≤ 350

0,2a+0,05b+0,04c+0,2f+0,1g ≤ 130

 

Трудоемкость производства этих изделий равна

 

(3,3a+0,4b+0,3c+1f+1,2g). Значит,

3,3a+0,4b+0,3c+1f+1,2g ≤ 1100

 

Итак, система ограничений имеет вид:

 

 

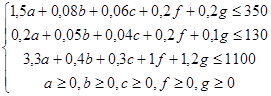
А прибыль будет выражена функцией

 

F=13000a+1300b+1200c+4300f+4450g

 

Чтобы найти решение задачи, воспользуемся MS Excel.

 

 

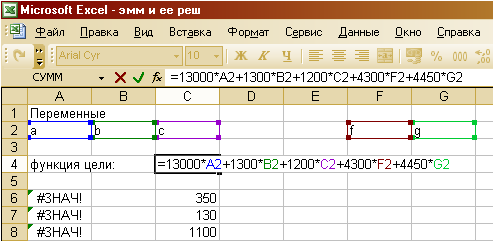
Целевую функцию зададим выражением:

 

=13000*A2+1300*B2+1200*C2+4300*F2+4450*G2

 

А систему ограничений так:

 

=1,5*A2+0,08*B2+0,065*C2+0,2*F2+0,2*G2

=0,2*A2+0,05*B2+0,04*C2+0,2*F2+0,1*G2

=3,3*A2+0,4*B2+0,3*C2+1*F2+1,2*G2

 

Открыв в меню «Сервис» команду «Поиск решения», заполним открывшееся окно: установим целевую ячейку, равную максимальному значению, определим ячейки-переменные, значения которых искомы, установим систему ограничений по имеющимся запасам сырья и располагаемой трудоемкости.

После этого в окне «Параметры» установим флажок в ячейку «Линейная модель» и выберем кнопку «Выполнить».

 

 

В результате решения получаем данные об оптимальном ассортименте продукции:

 

Переменные
160	0	20			429	114
функция цели:		4456000
349,9		350
130		130
1099,8		1100

Итак, чтобы получить максимальную прибыль 4 456 000 рублей при имеющихся запасах сырья и существующей трудоемкости получаемой продукции, предприятию следует производить 160 единиц товара вида А, 0 – вида В, 20 – вида С, 429 - вида F и 114 – вида G.

3. ПРИМЕНЕНИЕ ТЕОРИИ ТРАНСПОРТНОЙ ЗАДАЧИ К РАБОТЕ ООО «ДУБРОВЧАНКА+»