Применим неравенство Клаузиуса для описания необратимого кругового термодинамического процесса, изображенного на рис 1.
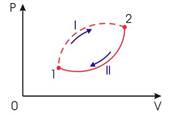
Рис.1. Необратимый круговой термодинамический процесс
Пусть процесс 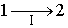 будет необратимым, а процесс
будет необратимым, а процесс 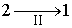 - обратимым. Тогда неравенство Клаузиуса для этого случая примет вид
- обратимым. Тогда неравенство Клаузиуса для этого случая примет вид
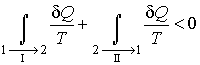 . .
|
Так как процесс 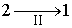 является обратимым, для него можно воспользоваться соотношением (3.53), которое дает
является обратимым, для него можно воспользоваться соотношением (3.53), которое дает
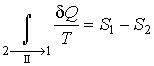 . .
|
Подстановка этой формулы в неравенство (3.55) позволяет получить выражение
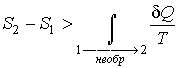 . .
|
Сравнение выражений (3.53) и (3.57) позволяет записать следующее неравенство
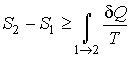 , ,
|
в котором знак равенства имеет место в случае, если процесс 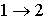 является обратимым, а знак больше, если процесс
является обратимым, а знак больше, если процесс 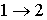 - необратимый.
- необратимый.
Неравенство (3.58) может быть также записано и в дифференциальной форме
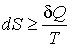 . .
|
Если рассмотреть адиабатически изолированную термодинамическую систему, для которой 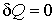 , то выражение (3.59) примет вид
, то выражение (3.59) примет вид
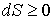
|
или в интегральной форме
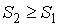 . .
|
 2020-01-14
2020-01-14 193
193








