Компоненты коммутирующей части схемы

Матрица, вектор	Размерность	Физический смысл компонент (передача КЧС)
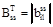
		от выхода i-го интегратора ко входу l-го интегратора
		от выхода i-го интегратора ко входу q-го усилителя
		от выхода j-го усилителя ко входу l-го усилителя
		от выхода j-го усилителя ко входу l-го интегратора
		от выхода i-го интегратора к нагрузке
		от выхода j-го усилителя к нагрузке
		от генератора ко входу i-го интегратора
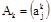
		от генератора ко входу j-го усилителя

 

Для обеспечения пассивности КЧС необходимо выполнить условия

 

                                 (2)

                         (3)

                                          (4)

 

гарантирующие возможность ее построения на базе резисторов, причем для любого h-го усилителя с фиксированным коэффициентом передачи возможна реализация отрицательных передач  путем использования неинвертирующего входа операционного усилителя (ОУ). В этом случае в неравенстве (2) учитываются модули соответствующих величин. Базисные структуры описываются диагональными матрицами

 

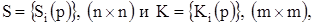         (5)

 

компоненты которых являются передаточными функциями реальных интеграторов и усилителей, поэтому

                     (6)

         (7)

 

где  – площадь и статический коэффициент усиления ОУ, положенного в основу i-го интегратора (j-го усилителя);  – коэффициент передачи на холостом ходу i-го (j-го) резисторного управителя.

Передаточная функция обобщенной структуры следует из системы векторно-матричных уравнений (1) и при переходе к блочным (клеточным) матрицам и векторам имеет вид:

 

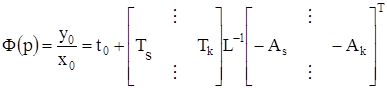.           (8)

 

Для идеальных ОУ  блочная матрица основной части системы может быть представлена следующим образом:

 

.                    (9)

 

При решении конкретных задач качественного характера удобным оказывается представление

               (10)

 

при этом векторы 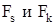, компоненты которых являются передаточными функциями на выходах интегрирующих и масштабных усилителей, определятся после обращения матрицы L_и по формулам Фробениуса [1] из следующих соотношений:

 

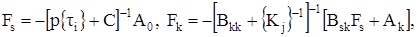 (11)

где  .

 

Воспользовавшись методом В.Н. Фаддеевой [6] для вычисления резольвенты матрицы , функцию (10) можно привести к дробно-рациональному виду

 

         (12)

 

где коэффициенты числителя и знаменателя определяются алгоритмом:

 

              (13)

 

Здесь 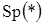 – след (сумма диагональных элементов) соответствую-щей матрицы.

Приведенный алгоритм позволяет на последнем шаге q = n осуществить контроль результата, т.к. . Однако он довольно чувствителен к ошибкам округления, поэтому при численных методах решения задачи необходимо предусмотреть перевод компонент матриц в числа с удвоенной точностью.