2020-01-14
115
Из математики известно, что интеграл равен площади криволинейной трапеции, ограниченной кривой f(x) осью Х и ординатами в точках а и b.
Для приближенного вычисления площади разобьём отрезок [а,b] на n части длинной h =(b-a)/n.
В точках разбиения проведем ординаты до пересечения с кривой y=f(x), а концы ординат соединим прямоугольными отрезками, тогда площадь криволинейного приближенного прямоугольника можно считать равной площади фигуры ограниченной ломанной линией aABb. Площадь этой фигуры, которую обозначим через S, равна сумме площадей прямоугольников.
S=h(y0+y1+y2+…+yn)
Таким образом, приближенное значение интеграла по формуле прямоугольников запишется в виде
Точность метода с постоянным шагом h примерно e 
h.
Метод трапеции
В этом методе начальные построения те же, только при вычислении площади криволинейной трапеции ординаты сверху соединяются ломаной линией.
 |
Получается множество прямоугольных трапеций. Площадь одной трапеции равна:
Sтр= 
.h
Отсюда: y 
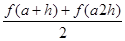. h + 
. h + … + 
. h =
= h . 
+ f(a + h) +…+ f(в-h) 
= 
+ 
Точность Е 
h2
