Тензор напряжений имеет следующие инварианты (invarient - неизменный), т.е. такие алгебраические комбинации компонентов, которые не меняют своих значений при повороте осей тензора (осей координат):
I 1(T н) = sx + sy + sz,
I 2(T н) = sx.sy + sy.sz + sz.sx - txy2 - txz2 - tyz2,
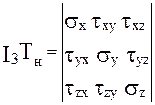
Величина
sср = I 1(T н) /3 = ( sx + sy + sz ) / 3
определяет среднее нормальное (гидростатическое) напряжение в «точке» и вызывает изменение объёма этой «точки».
Напряженное состояние в «точке» можно представить в виде суммы двух напряженных состояний, описываемых шаровым тензором и тензором-девиатором:
T н = T нш + T нд.
Шаровым тензором называется тензор вида
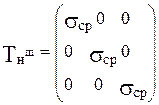
он вызывает изменение только объёма «точки».
Тензор-девиатор T нд определяет величину отклонения от гидростатического состояния и имеет следующие компоненты:
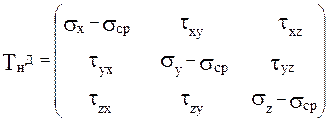
Легко убедиться в том, что первый инвариант тензора-девиатора равен нулю:
(sx -sср) + (sy - sср) + (sz - sср) = 0.
Это означает, что объёмные деформации, вызываемые тензором-девиатором, равны нулю. Касательные напряжения тензора-девиатора вызывают изменения формы «точки».
Произвольное напряженное состояние, в котором находится тело, можно представить в виде суммы двух напряженных состояний: первое представляет собой гидростатическое сжатие тела напряжением sср, а второе напряженное состояние наложено на первое и представляет собой состояние сдвига, обеспечиваемое тензором-девиатором напряжений.
Напряженное состояние в точке определено, если известны компоненты тензора напряжений T нш и тензора-девиатора напряжений T нд.
В механике сплошной среды показывается, что любой тензор напряжений может быть приведен к самому простому виду:

где s1, s2, s3 - главные нормальные напряжения. Они перпендикулярны друг другу и между ними выполняется неравенство s1 > s2 > s3.
Шаровой тензор напряжений и тензор-девиатор напряжений, выраженные через главные нормальные напряжения, имеют вид:
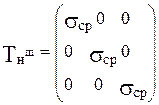
где sср = (s1 + s2 + s3) / 3 и

 Главные касательные напряжения тензора напряжений T н выражаются через главные нормальные напряжения
Главные касательные напряжения тензора напряжений T н выражаются через главные нормальные напряжения
t1 = (s2-s3)/2, t2 = (s1-s3)/2, t3 = (s1-s2)/2,
векторы которых лежат на трех парах взаимно перпендикулярных плоскостей, делящих пополам углы между главными осями тензора напряжений.
Величина главных касательных напряжений тензора напряжений T н совпадает с величиной главных касательных напряжений тензора-девиатора напряжений T нд. В справедливости этого легко убедиться, выразив главные касательные напряжения тензора-девиатора через главные нормальные напряжения s1 - sср, s2 - sср, s3 - sср:
t1д = [(s2 - sср) - (s3 - sср)] / 2 = (s2 - s3)/2 = t1,
t2д = [(s1 - sср) - (s3 - sср)] / 2 = (s1 - s3)/2 = t2,
t3д = [(s1 - sср) - (s2 - sср)] / 2 = (s1 - s2)/2 = t3.
В механике сплошной среды большую роль играет первый инвариант тензора напряжений I 1(T н) и второй инвариант девиатора напряжений I 2(T нд). Через главные нормальные напряжения они имеют следующий вид:
I 1(T н) = (s1 + s2 + s3),
I 2(T нд) = [ (s1-s2)2 + (s2-s3)2 + (s1-s3)2 ] / 6.
Через второй инвариант девиатора напряжений вводится понятие интенсивности напряжений:
— интенсивность нормальных напряжений
si = [ 3. I 2(T нд) ] 0,5, (1)
—интенсивность касательных напряжений
ti = [I 2(T нд) ] 0,5. (2)
Через главные нормальные напряжения величины si, ti выражаются следующим образом:
si = [ (s1-s2)2 + (s2-s3)2 + (s3-s1)2 ] 0.5 / 2 0.5,
ti = [ (s1-s2)2 + (s2-s3)2 + (s3-s1)2 ] 0.5 / 60.5.
Напряженное состояние в любой точке деформируемого тела определено, если в любой точке этого тела известны значения среднего нормального напряжения sср и интенсивности касательного напряжения ti.
Угол вида напряженного состояния, параметр Лоде. Для характеристики напряженного состояния используются еще две инвариантные характеристики, которые определяются через третий инвариант девиатора напряжений I 3(T нд) = (s1-sср)(s2-sср)(s3-sср):
— угол вида напряженного состояния j(s):
tg j(s) = (s1 —s2)30.5 / (s1 + s2 —2s3),
— параметр Лоде m(s):
m(s) = (2s2 —s1 —s3) / (s1 —s3).
Величины j(s) и m(s) связаны друг с другом соотношением
m(s) = 30.5 ctg( j(s) + p/3 ).
Величина параметров j(s) и m(s) изменяется в пределах
p/3 ³ j(s) ³ 0, - 1≤ m(s) ≤ +1.
Напряженные состояния являются подобными, когда параметры j(s) и m(s) этих состояний равны. Если в процессе нагружения параметр Лоде m(s) остается постоянным, то нагружение считается простым.
Вектор перемещения (вектор деформации) и деформированное состояние в точке. Приложение к твердому телу напряжений и его деформирование приводит к возникновению в теле поля перемещений: каждая точка тела перемещается из одного положения в другое. Такое перемещение точки под действием сил из начального положения в конечное характеризуется вектором перемещения (вектором деформации) U. В векторном виде вектор деформации представим следующим образом:
U = r' — r,
где r', r -радиус-векторы, характеризующие положение рассматриваемой
 |
точки после и до приложения сил, соответственно. Вектор U имеет следующие проекции на оси координат X, Y, Z, соответственно: u, v, w.
Полное перемещение деформируемых точек в трехмерном пространстве выражается формулой d = (u 2 + v 2 + w 2)0,5 и является непрерывной функцией координат.
Деформированное состояние в «точке», также как и напряженное состояние, описывается тензором, отвечающим за изменение геометрии рассматриваемой «точки»: изменение её объёма и формы.
Представим «точку» в виде элементарного куба. Рассмотрим одну грань куба, лежащую в плоскости YX (Рис. 3). До механического нагружения «точки» грань куба ОАБС имеет следующие размеры: ОА = D y, ОС = D x. После деформации отрезки ОА, ОС изменят не только свои размеры, но и направления. По этой причине деформация «точки»слагается из линейных (ex, ey, ez) и сдвиговых (угловых) (gxy, gxz, gyx, gyz, gzx, gzy) деформаций. Соответственно этому и тензор деформаций состоит из линейных и сдвиговых компонент:

Деформация, соответствующая нормальным напряжениям тензора напряжения, выражается через относительное изменение линейного размера тела l. Линейная деформация может быть абсолютной и в этом случае она опреде-ляется формулой
(l к - l н ) = D l,
где l к —линейный размер тела после деформирования, l н —начальный линейный размер тела, и относительной
e = D l / l н.
Принято считать относительную линейную деформацию положительной, если она происходит при сжатии, и отрицательной - при растяжении тела.
Линейная относительная деформация, происходящая по направлению действия силы, называется п родольной, а перпендикулярно действию силы — поперечной.
Сторона ОС деформируемой «точки» кубика преобразуется в отрезок ОС1, проекция которого на ось X равна величине (D x + D u), где D u = (d u / d x)D x, D x >> D u. Отсюда следует, что относительная линейная деформация отрезка ОС, измеряемая в направлении оси X, определится следующим выражением
ex = { Dx — [ D x + (‑D u) ]} / D x = d u/ d x.
Числитель в написанной формуле обозначает абсолютную деформацию стороны ОС куба. Знак «минус» перед величиной D u обозначает, что рассматривается деформация растяжения тела (при сжатии тела в этой формуле берется знак «плюс».
Линейная относительная деформация элементарного куба в направлении осей Y, Z обозначаются аналогичным образом: ey, ez. Величина этих деформаций выражается через компоненты вектора перемещения v, w:
ey = dv/dy, ez = dw/dz,
Угловые (сдвиговые) деформации в теле возникают при действии касательных напряжений. Сдвиговая деформация физически представляет собой величину изменения прямого угла между гранями элементарного куба при его деформировании. Если рассмотреть, например, одну грань куба, находящуюся в плоскости YX (Рис. 3), то величина угла a, определяющего отклонение направления отрезка ОС1 от его первоначального направления ОС, определится проекциями D u и D v
tg a = D v / (D x + D u)» d v/ d x,
т.е. угловая деформация gxy выражается как градиент смещения
gxy = d v/ d x.
(Первая буква индекса обозначает ось, от которой происходит движение, вторая буква — к какой оси осуществляется поворот).
Угол b характеризует изменение направления отрезка ОА. Величина угла b определяет угловую деформацию gyx и выражается через проекции отрезка ОА1 на оси X (проекция u) и Y (проекция v):
gyx = tg b = D u / (D y + D v)» d u/ d y.
Суммарное изменение первоначально прямого угла между отрезками ОС и ОА определяется углом y = a + b.
Совместное искажение первоначально прямых углов описывается суммой
tg a + tg b» tg (a + b) = tg y = d v/ d x + d u / d y
или
gxy = gyx = tg (a + b) / 2 = y / 2.
Если появление очень малых углов a и b интерпретировать как вращение тела, то угол поворота каждой из рассматриваемых сторон будет равен величине y/2.
Связь между компонентами вектора смещения и компонентами тензора деформации определяется геометрическими уравнениями (уравнения Коши):
ex = du/dx, ey = dv/dy, ez = dw/dz,
gxz = dw/dx + du/dz, gxy = dv/dx + du/dy, gyz = dw/dy + dv/dz.
Физический смысл геометрических уравнений (уравнений Коши) заключается в том, что деформируемое тело является сплошным до, во время и после деформирования. Другими словами, деформирование тела происходит без разрыва вектора перемещения U и, естественно, без разрыва его проекций u, v, w на оси координат.
Тензор деформации T д, так же как тензор напряжений, имеет три инварианта I 1(T д), I 2(T д), I 3(T д), аналогичные по строению инвариантам тензора напряжений:
I 1(T д) = ex + ey + ez,
I 2(T д) = ex.ey + ey.ez + ez.ex - gxy2 - gxz2 - gyz2,

Тензору напряжений, выраженному через главные нормальные напряжения s1, s2, s3, соответствует тензор деформации T д вида

где e1, e2, e3 —есть главные линейные деформации; своим появлением они обязаны действию главных нормальных напряжений.
Разности g1 = e2 —e3, g2 = e3 —e1, g3 = e1 —e2 определяют величину главных сдвигов.
Как и в случае с тензором напряженного состояния, тензор деформации можно разложить на два тензора, отвечающих за изменение объёма и формы «точки»:
T д = T дШ + T дД,
где T дШ —шаровой тензор, имеющий вид:

T дД —тензор-девиатор, имеющий вид:

где eср = ( ez+ ey+ ex ) /3 — средняя линейная относительная деформация. Шаровый тензор определяет изменение объема «точки», а тензор-девиатор отвечает за изменение формы «точки».
Величина
ev = ez + ey + ex
характеризует относительное изменение объёма DV / V элементарного куба, «точки». Этот вывод следует из следующего мысленного опыта. Если к «точке», имеющей форму куба, приложить три взаимно равных сжимающих напряжения, то «точка» будет находиться в состоянии гидростатического сжатия: P = sx = sy = sz, а касательные напряжения в ней будут равны нулю. Приложенные нормальные напряжения вызовут укорочение ребер куба, а значит и уменьшение его объёма. Если первоначальную длину ребра куба принять равной единице, то относительное изменение объёма такого куба ev будет равно следующей величине:
ev = D V/V = [ (начальный объём)-(полученный объём) ]/ (начальный объём) =
[1 - (1‑ex)(1‑ey)(1‑ez) ] / 1.
Если не принимать во внимание величины второго и третьего порядка малости (т.е. произведения типа ezey, exezey), то легко получается окончательная формула
ev = ez + ey + ex.
Разделив правую и левую части этого равенства на число 3, получим связь между средней линейной относительной деформацией и относительной объемной деформацией
eср = ev / 3.
Первый инвариант тензора девиатора, т.е. величина
ex - eср + ey - eср + ez - eср
тождественно равна нулю. Физически это означает, что сумма диагональных напряжений тензора девиатора не вызывает изменения объёма деформируемой точки.
Шаровой тензор деформаций T дш, выраженный через главные линейные деформации, имеет вид:

где eср = ( e1 + e2 + e3 ) / 3, а тензор-девиатор T дд деформаций задается матрицей следующего содержания:

В механике сплошной среды (в теории пластичности) большое значение имеет второй инвариант девиатора деформаций
I 2(T дд) = [( e1 - e2 ) 2 + ( e2 - e3 ) 2 + ( e3 - e1 ) 2 ] / 6,
который является суммарной характеристикой изменения формы деформируемого тела. Через второй инвариант девиатора деформаций I 2(T дд) выражаются интенсивность линейных деформаций ei и интенсивность деформаций сдвига gi:
ei = 2×I2(Тдд) / ×3,
gi = 2×I2(Тдд).
Через главные линейные деформации приведенные величины выражаются следующим образом:
ei = ×2. [ ( e1 - e2 ) 2 + ( e2 - e3 ) 2 + ( e3 - e1 ) 2 ] 0.5 / 3, (3)
gi = (2/3)0,5. [ ( e1 - e2 ) 2 + ( e2 - e3 ) 2 + ( e3 - e1 ) 2 ] 0.5. (4)
Резюме: Деформация тела заключается в изменении формы, вызванном
 2020-01-14
2020-01-14 221
221








