1. Дифференциальными уравнениями называют уравнения, которые содержат неизвестную функцию, её производные и аргументы.
Обыкновенным называется дифференциальное уравнение, в котором неизвестная функция является функцией одной переменной. Если неизвестная функция является функцией многих переменных, то соответствующее уравнение называется дифференциальным уравнением в частных производных.
Порядком дифференциального уравнения называется наивысший порядок производной, которая входит в это уравнение.
Пример 7.1.
1)  - обыкновенное дифференциальное уравнениеІ порядка.
- обыкновенное дифференциальное уравнениеІ порядка.
2)  - обыкновенное дифференциальное уравнениеІІІ порядка.
- обыкновенное дифференциальное уравнениеІІІ порядка.
3)  +
+ 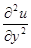 =0 - дифференциальное уравнениев частных производных ІІ порядка (уравнение Лапласа).
=0 - дифференциальное уравнениев частных производных ІІ порядка (уравнение Лапласа).
Далее будем рассматривать только обыкновенные дифференциальные уравнения.
Наиболее общий вид дифференциального уравнения І порядка такой:
F (x, у, у ’)=0. (7.1)
Решением этого уравнения на некотором промежутке называется дифференцированная на этом промежутке функция  , которая при подстановке её в уравнение превращает его в тождество.
, которая при подстановке её в уравнение превращает его в тождество.
Пример 7.2. Решить уравнение  .
.
Решение.
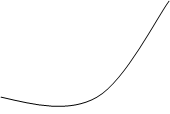
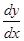 = у,
= у,  =
=  , ln
, ln 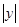 = x+ ln
= x+ ln 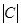 , у=Сех.
, у=Сех.
Получили множество решений.

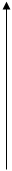 у
у
С =2
С =1
2
 1 С =0
1 С =0

 0
0
-1 С = -1
-2
С =-2
Функция  , где С – произвольная постоянная, называется общим решением уравнения (7.1) в области D, если:
, где С – произвольная постоянная, называется общим решением уравнения (7.1) в области D, если:
1) функция  является решениемуравнения (7.1) для всех значений переменной С из некоторого множества;
является решениемуравнения (7.1) для всех значений переменной С из некоторого множества;
2) для произвольной точки (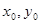 )
)  существует единственное значение С=С 0, при котором функция
существует единственное значение С=С 0, при котором функция 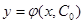 удовлетворяет начальному условию
удовлетворяет начальному условию 
Решение 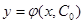 , полученное из общего решения при С=С 0, называется частным решением уравнения (7.1).
, полученное из общего решения при С=С 0, называется частным решением уравнения (7.1).
С геометрической точки зрения решение  определяет некоторое бесконечное множество кривых, которые называются интегральными кривыми данного уравнения. Частное решение определяет только одну интегральную кривую, которая проходит через точку с координатами (
определяет некоторое бесконечное множество кривых, которые называются интегральными кривыми данного уравнения. Частное решение определяет только одну интегральную кривую, которая проходит через точку с координатами (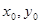 ).
).
Если общее решение уравнения (7.1) найдено в неявном виде Ф(х, у, С)=0, то такое решение называют общим интегралом дифференциального уравнения; равенство Ф(х, у, С 0)=0 называют частным интегралом дифференциального уравнения.
Значит, для уравнения (7.1) можно поставить две задачи:
1) найти общее решение  уравнения (7.1);
уравнения (7.1);
2) найти частное решение  уравнения (7.1), которое удовлетворяет начальному условию
уравнения (7.1), которое удовлетворяет начальному условию  .
.
Вторая задача называется задачей Коши для обыкновенного дифференциального уравненияІ порядка.
Пример 7.3. Решить задачу Коши
 , у (0)=2.
, у (0)=2.
Решение. Сначала ищем общее решение дифференциального уравнения: у=Сех.
Из начального условия имеем: 2= Се 0 
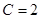 .
.
Решением задачи Коши является такая функция: у= 2 ех.
Если уравнение (7.1) можно решить относительно у’, то его записывают в виде

и называют уравнением первого порядка, решенным относительно производной, или уравнением в нормальной форме.
Теорема 7.1 (существования и единственности решения задачи Коши). Если функция  непрерывна в некоторой области D, которая содержит точку М
непрерывна в некоторой области D, которая содержит точку М  (
(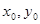 ), то задача Коши
), то задача Коши
 ,
, 
имеет решение. Если, кроме этого, в точке М  непрерывна частная производная
непрерывна частная производная  , то это решение единственное.
, то это решение единственное.
Процесс нахождения решений дифференциальных уравнений называется интегрированием этих уравнений. Если этот процесс сводится к алгебраическим операциям и вычислению конечного числа интегралов и производных, то говорят, что уравнение интегрируется в квадратурах. Однако класс таких уравнений очень ограничен. Поэтому для решения дифференциальных уравнений широко применяют разные приближённые методы интегрирования дифференциальных уравнений с использованием вычислительной техники.
Рассмотрим некоторые типы уравнений, интегрируемых в квадратурах.
2. Дифференциальное уравнение вида
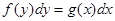
называется дифференциальным уравнением с разделёнными переменными.
Чтобы найти его общее решение, достаточно проинтегрировать обе его части.
 .
.
Дифференциальное уравнение вида

называется дифференциальным уравнением с разделяющимися переменными.
Чтобы найти его общее решение, надо сначала отделить переменные

а затем проинтегрировать
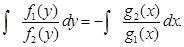
Пример 7.4. Найти общее решение уравнения

Решение. Сначала отделим переменные

 ,
,
а затем проинтегрируем
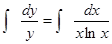 ,
,  , у=С ln x.
, у=С ln x.
3. Функция  называется однородной функцией п -го измерения относительно переменных х и у, если для произвольного числа
называется однородной функцией п -го измерения относительно переменных х и у, если для произвольного числа  выполняется тождество
выполняется тождество

Пример 7.5.
1)  =
=  ,
, 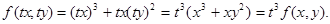
 - однородная функция третьего измерения.
- однородная функция третьего измерения.
2)  =
= 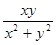 - однородная функция нулевого измерения.
- однородная функция нулевого измерения.
Уравнение y’=  называется однородным дифференциальным уравнением первого порядка, если функция
называется однородным дифференциальным уравнением первого порядка, если функция  является однородной функцией нулевого измерения, то есть, если
является однородной функцией нулевого измерения, то есть, если
 (7.2)
(7.2)
Очевидно, уравнение вида

будет однородным тогда и только тогда, когда функции Р (х, у) и Q (х, у), будут однородными функциями одного и того же измерения. Например, уравнение

однородное. Считая, в соотношении (7.2)  , получим
, получим
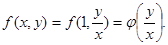
Поэтому можно дать ещё одно определение однородного уравнения: однородным дифференциальным уравнением называется уравнение вида
 (7.3)
(7.3)
Применим в уравнении (7.3) подстановку
 ,
,  ,
, 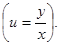
Тогда получим уравнение с разделяющимися переменными
 ,
,
которое всегда интегрируется в квадратурах:
 ,
,
 .
.
После интегрирования надо сделать обратную замену, то есть вместо и нужно подставить 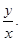
Вывод. Однородные дифференциальные уравнения первого порядка всегда сводятся к уравнениям с разделяющимися переменными подстановкой  ,
, 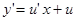 .
.
Пример 7.6. Найти общее решение уравнения
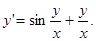
Решение. Применим подстановку  ,
,  . Тогда получим
. Тогда получим
 ,
,
 ,
,  ,
,
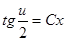 ,
, 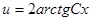 ,
, 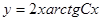 .
.
Пример 7.7. Решить задачу Коши
 , у (1)=2.
, у (1)=2.
Решение. Поскольку обе функции


однородные измерения два, то данное уравнение однородное. Запишем его в виде

и применим подстановку  ,
, 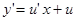 . Тогда получим
. Тогда получим
 ,
, 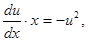
 ,
,  ,
,  .
.
Из начального условия найдём постоянную интегрирования:
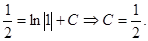
Подставив найденное значение С в общее решение, получим решение задачи Коши:

 2020-01-14
2020-01-14 106
106








