Полиномиальная арифметика

Рассмотрим вероятностный алгоритм, позволяющий эффективно находить решения полиномиальных сравнений по простому модулю. Пусть p – простое число, которое предполагается большим, и f (x)ÎZ[ x ] – многочлен, степень которого предполагается ограниченной. Задача состоит в отыскании решений сравнения

f (x) º 0 (mod p).                                                        (1)

Например, речь может идти о решении квадратичных сравнений, если степень многочлена f (x) равна 2. Другими словами, мы должны отыскать в поле F _p = Z/ p Z все элементы, удовлетворяющие уравнению f (x) = 0.

Согласно малой теореме Ферма, все элементы поля F _p являются однократными корнями многочлена x^p - x. Поэтому, вычислив наибольший общий делитель d (x) = (x^p - x, f (x)), мы найдём многочлен d (x), множество корней которого в поле F _p совпадает с множеством корней многочлена f (x), причём все эти корни однократны. Если окажется, что многочлен d (x) имеет нулевую степень, т. е. лежит в поле F _p, это будет означать, что сравнение (1) не имеет решений.

Для вычисления многочлена d (x) удобно сначала вычислить многочлен c (x)º x^p (mod f (x)), пользуясь алгоритмом, подобным описанному выше алгоритму возведения в степень (напомним, что число p предполагается большим). А затем с помощью аналога алгоритма Евклида вычислить d (x) = (c (x) – x, f (x)). Всё это выполняется за полиномиальное количество арифметических операций.

Таким образом, обсуждая далее задачу нахождения решений сравнения (1) мы можем предполагать, что в кольце многочленов F _p [ x ] справедливо равенство

f (x) = (x – a₁)*…*(x – a_n), a_i ÎF _p, a_i ¹ a_j.

3. 1 Алгоритм нахождения делителей многочлена f (x) в кольце F _p [ x ]

1. Выберем каким-либо способом элемент d Î F _p.

2. Вычислим наибольший общий делитель

g (x) = (f (x), (x + d)^(p-1)/2 – 1).

3. Если многочлен g (x) окажется собственным делителем f (x), то многочлен f (x) распадается на два множителя и с каждым из них независимо нужно будет проделать все операции, предписываемые настоящим алгоритмом для многочлена f (x).

4. Если окажется, что g (x) = 1 или g (x) = f (x), следует перейти к шагу 1 и, выбрав новое значение d, продолжить выполнение алгоритма.

Количество операций на шаге 2 оценивается величиной O (ln p), если вычисления проводить так, как это указывалось выше при нахождении d (x). Выясним теперь, сколь долго придётся выбирать числа d, пока на шаге 2 не будет найден собственный делитель f (x).

Количество решений уравнения (t + a₁)^{( p – 1)/2} = (t + a₂)^{( p – 1)/2} в поле F _p не превосходит (p -3)/2. Это означает, что подмножество D Ì F _p, состоящее из элементов d, удовлетворяющих условиям

(d + a₁)^{(p – 1)/ 2} ¹ (d + a₂)^{(p – 1)/ 2}, d ¹ - a₁, d ¹ - a₂,

состоит не менее чем (p – 1)/2 из элементов. Учитывая теперь, что каждый ненулевой элемент b ÎF _p удовлетворяет одному из равенств b ^{( p – 1)/2} = 1, либо   b ^{( p – 1)/2} = –1, заключаем, что для d Î D одно из чисел a₁, a₂ будет корнем многочлена (x + d) ^{( p – 1)/2} – 1, а другое – нет. Для таких элементов d многочлен, определённый на шаге 2 алгоритма, будет собственным делителем многочлена f (x).

Итак, существует не менее (p –1)/2 «удачных» выборов элемента d, при которых на шаге 2 алгоритма многочлен f (x) распадается на два собственных множителя. Следовательно, при «случайном» выборе элемента d Î F _p, вероятность того, что многочлен не разложится на множители после k повторений шагов алгоритма 1-4, не превосходит 2^{- k} . Вероятность с ростом k убывает очень быстро. И действительно, на практике этот алгоритм работает достаточно эффективно.

Заметим, что при оценке вероятности мы использовали только два корня многочлена f (x). При n > 2 эта вероятность, конечно, ещё меньше. Более тонкий анализ с использованием оценок А. Вейля для сумм характеров показывает, что вероятность для многочлена f (x) не распасться на множители при однократном проходе шагов алгоритма 1-4 не превосходит 2^{- n} + O (p ^-1/2). Здесь постоянная в O (.) зависит от n. В настоящее время известно элементарное доказательство оценки А. Вейля.

Если в сравнении (1) заменить простой модуль p составным модулем m, то задача нахождения решений соответствующего сравнения становится намного более сложной. Известные алгоритмы её решения основаны на сведении сравнения к совокупности сравнений (1) по простым модулям – делителям m, и, следовательно, они требуют разложения числа m на простые сомножители, что, как уже указывалось, является достаточно трудоёмкой задачей.

Произведение и возведение в степень многочленов, заданных массивами

Условимся представлять многочлены массивами, индексированными, начиная с 0, в которых элемент с индексом i означает коэффициент многочлена степени i

Type

Polynome =array [1.. Nmax ] of Ring_Element;

Следующий алгоритм даёт функцию умножения двух многочленов и, где многочлен степени (который даёт результат в конце алгоритма) должен быть предварительно инициализирован нулём.     

for i:= 0 to deg P do

for j:= 0 to deg Q do

       R [ i + j ]:= R [ i + j ]+ P [ i ]* Q [ i ];

Изучая предыдущий алгоритм, устанавливаем, что его сложность как по числу перемножений, так и сложений, равна произведению высот двух многочленов: (deg P + 1)(deg Q + 1), но в этом алгоритме, который не учитывает случай нулевых коэффициентов, можно рассматривать высоту многочлена как число всех коэффициентов. Значит, возможно улучшить предыдущий алгоритм, исключив все ненужные перемножения:

for i:= 0 to deg P do

if P [ i ] ¹ 0 then

for j:= 0 to deg Q do

if Q [ j ] ¹ 0 then

R [i+j]:= R [ i + j ]+ P [ i ] Q [ i ];

Очень просто вычислить сложность алгоритма возведения в степень последовательными умножениями, если заметить, что когда P – многочлен степени d, то Pⁱ – многочлен степени id. Если обозначить C_mul (n) сложность вычисления Pⁿ, то рекуррентное соотношение C_mul (i + 1) = C_mul (i) + (d +1)(id +1) даёт нам:

 

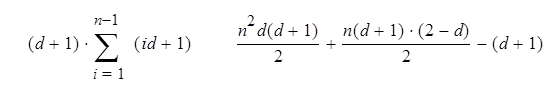  C_mul (n) =                              =

 

 

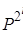
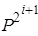Что касается возведения в степень с помощью дихотомии (т.е. повторяющимися возведениями в квадрат), вычисления несколько сложнее: зная, вычисляем     с мультипликативной сложностью. Как следствие имеем:

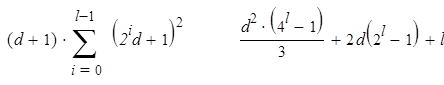C_sqr (2 ^l) =                                        =                                          =

=

 

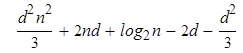Предварительное заключение, которое можно вывести из предыдущих вычислений, складывается в пользу дихотомического возведения в степень: если n есть степень двойки (гипотеза ad hoc), этот алгоритм ещё выдерживает конкуренцию, даже если эта победа гораздо скромнее в данном контексте (n ² d ²/3 против n ² d ²/2), чем когда работаем в Z/ p Z (2log₂ n против n).

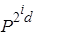
Но мы не учли корректирующие перемножения, которые должны быть выполнены, когда показатель не является степенью двойки. Если n = 2l+1 – 1, нужно добавить к последовательным возведениям в квадрат перемножения всех полученных многочленов. Умножение многочлена       степени (2 ⁱ -1) d на многочлен               степени 2 ⁱd вносит свой вклад из ((2 ⁱ – 1) d + 1)(2 ⁱ d + 1) умножений, которые, будучи собранными по всем корректирующим вычислениям, дают дополнительную сложность:

=                                                              =

                  

                                 =                    

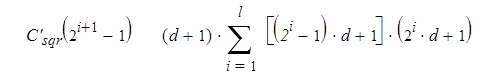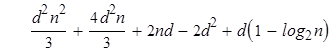
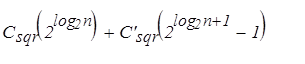
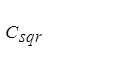
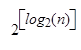Теперь можно заключить, что дихотомическое возведение в степень не всегда является лучшим способом для вычисления степени многочлена с помощью перемножений многочленов. Число перемножений базисного кольца, которые необходимы, C_sqr (n), - в действительности заключено между    (        ) и                                                т.е. между n ² d ²/3 и 2 n ² d ²/3, тогда как простой алгоритм требует всегда n ² d ²/2 перемножений. В частности, если исходный многочлен имеет степень, большую или равную 4, возведение в степень наивным методом требует меньше перемножений в базисном кольце, чем бинарное возведение в степень, когда n имеет форму 2 ^l – 1.

Можно довольно просто доказать, что если n имеет вид 2 ^l +2 ^{l – 1} + c (выражения, представляющие двоичное разложение n), то метод вычисления последовательными перемножениями лучше метода, использующего возведение в квадрат (этот последний метод требует корректирующего счёта ценой, по крайней мере, n ² d ²/9). Всё это доказывает, что наивный способ является лучшим для этого класса алгоритмов, по крайней мере, в половине случаев.

Действительно, МакКарти [3] доказал, что дихотомический алгоритм возведения в степень оптимален среди алгоритмов, оперирующих повторными умножениями, если действуют с плотными многочленами (антоним к разреженным) по модулю m, или с целыми и при условии оптимизации возведения в квадрат для сокращения его сложности наполовину (в этом случае сложность действительно падает приблизительно до n ² d ²/6 + n ² d ²/3 = n ² d ²/2).