Небольшие оптимизации для произведений многочленов

В принципе вычисление произведения двух многочленов степеней n и m соответственно требует (n +1)(m +1) элементарных перемножений. Алгоритм оптимизации возведения в квадрат состоит просто в применении формулы квадрата суммы:

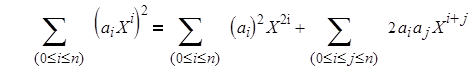что даёт n +1 умножений для первого члена и n (n +1)/2 – для второго, или в целом (n +1)(n +2)/2 умножений, что близко к половине предусмотренных умножений, когда n большое.

Для произведения двух многочленов первой степени P = aX + b и Q = cX + d достаточно легко находим формулы U = ac, W = bd, V = (a + b)(c + d) и PQ = = UX ² + (V – U – W) X + W, в которых появляются только три элементарных умножения, но четыре сложения. Можно рекурсивно применить этот процесс для умножения двух многочленов P и Q степени 2 ^l – 1, представляя их в виде и применяя предыдущие формулы для вычисления PQ в зависимости от A, B, C и D, где каждое произведение AB, CD и (A + B)(C + D) вычисляется с помощью рекурсивного применения данного метода (это метод Карацубы). Всё это даёт мультипликативную сложность M (2 ^l)и аддитивную сложность A (2 ^l)такие, что:

M (2 ^l) = 3 M (2 ^l^{– 1}),…, M (2) = 3 M (1), M (1) = 1,

A (2 ^l) =3 A (2 ^l^{– 1}) + 3*2 ^l,…, A (2) = 3 A (1) + 6, A (1) = 1.

В этой последней формуле член 3*2 ^l представляет собой число элементарных сложений, необходимых, чтобы сделать два сложения многочленов степени 2 ^{l – 1} – 1 (a + b и c + d) и два вычитания многочленов степени 2 ^l – 1 (U – V – W). Суммируя каждое из этих выражений, находим для n, являющегося степенью двойки:

M (n) = n ^log3/log2» n ^1,585 и A (2) =7 n ^log3/log2 – 6 n.

К сожалению, этот принцип остаётся теоретическим, и на его основе нужно построить итерационный алгоритм, чтобы получить разумную эффективность (цена управления рекурсией очень велика).

Вычисление многочленов

Рассмотрим общую задачу вычисления многочлена n -й степени

u (x) = u_nxⁿ + u_{n –} ₁ x^{n –} ¹ +... + u ₁ x + u ₀, u_n ¹ 0, (1)

Схема Горнера

u (x) = (…(u_nx + u_n _{– 1}) x + …) x + u ₀. (2)

Весь этот процесс требует n умножений и n сложений.

Было предложено несколько обобщений схемы Горнера. Посмотрим сначала, как вычисляется в случае, когда – комплексное число, а коэффициенты вещественны. Комплексное сложение и умножение можно очевидным образом свести к последовательности обычных операций над вещественными числами:

вещественное + комплексное требует 1 сложение,

комплексное + комплексное требует 2 сложения,

вещественное * комплексное требует 2 умножения,

комплексное * комплексное требует 4 умножения и 2 сложения

или 3 умножения и 5 сложений.

Следовательно, схема Горнера (2) требует 4 n – 2 умножений и 3 n – 2 сложений или 3 n – 1 умножений и 6 n – 5 сложений для вычисления u (z), когда z комплексное. Вот другая процедура для вычисления u (x + iy):

a ₁ = u_n, b ₁ = u_{n –} ₁, r = x + x, s = x ² + y ²; (3)

a_j = b_{j –} ₁ + ra_{j –} ₁, b_j = u_{n – j} – sa_j _–1, 1 < j £ n.

Легко доказать индукцией по n, что u (z) = za_n + b_n. Эта схема требует 2 n + 2 умножений и 2 n + 1 сложений, так что при n ³ 3 она лучше схемы Горнера.

Рассмотрим процесс деления многочлена u (x) на многочлен x – x₀. В результате такого деления мы получаем u (x) = (x – x ₀) q (x) + r (x); здесь deg(r) < 1, поэтому r (x) есть постоянная, не зависящая от x и u (x ₀) = 0* q (x ₀) + r = r. Анализ этого процесса деления показывает, что вычисления почти те же самые, что в схеме Горнера для определения u (x ₀). Аналогично, когда мы делим u (z) на многочлен (z – z ₀)(z – z ₀) = z ² – 2 x ₀ z + x ₀² + y ₀², то соответствующие вычисления эквивалентны процедуре (3); мы получаем

u (z) = (z – z ₀)(z – z ₀)q(z) + a_nz + b_n;

следовательно,

u (z ₀) = a_nz ₀ + b_n.

Вообще, когда мы делим u (x) на, f (x) получая u (x) = f (x) q (x) + r (x), то из равенства f (x ₀) = 0 следует u (x ₀) = r (x ₀); это наблюдение ведёт к дальнейшим обобщениям правила Горнера. Мы можем положить, например, f (x) = x ² – x ₀²; это даст нам схему Горнера «второго порядка»