Алгоритмы нахождения НОД

Алгоритм Евклида

Алгоритм Евклида — алгоритм для нахождения наибольшего общего делителя двух целых чисел или наибольшей общей меры двух однородных величин.

Этот алгоритм не был открыт Евклидом, так как упоминание о нём имеется уже в Топике Аристотеля. В «Началах» Евклида он описан дважды — в VII книге для нахождения наибольшего общего делителя двух натуральных чисел и в X книге для нахождения наибольшей общей меры двух однородных величин. В обоих случаях дано геометрическое описание алгоритма, для нахождения «общей меры» двух отрезков.

Историками математики (Цейтен и др.) было выдвинуто предположение, что именно с помощью алгоритма Евклида (процедуры последовательного взаимного вычитания) в древнегреческой математике впервые было открыто существование несоизмеримых величин (стороны и диагонали квадрата, или стороны и диагонали правильного пятиугольника). Впрочем, это предположение не имеет достаточных документальных подтверждений. Алгоритм для поиска наибольшего общего делителя двух натуральных чисел описан также в I книге древнекитайского трактата Математика в девяти книгах.

Ряд математиков средневекового Востока (Сабит ибн Курра, ал-Махани, Ибн ал-Хайсам, Омар Хайям) попытались построить на основе алгоритма Евклида теорию отношений, альтернативную по отношению теории отношений Евдокса, изложенной в V книге «Начал» Евклида. Согласно определению, предложенному этими авторами, четыре величины, первая ко второй и третья к четвёртой, имеют между собой одно и то же отношение, если при последовательном взаимном вычитании второй величины в обеих парах на каждом шаге будут получаться одни и те же неполные частные.

Алгоритм Евклида для целых чисел

Пусть a и b целые числа, не равные одновременно нулю, и последовательность чисел

определена тем, что каждое rk — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть

a = bq0 + r1

b = r1q1 + r2

r1 = r2q2 + r3

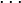
rk − 2 = rk − 1qk − 1 + rk

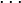
rn − 1 = rnqn

Тогда НОД(a,b), наибольший общий делитель a и b, равен rn, последнему ненулевому члену этой последовательности.

Существование таких r1,r2,..., то есть возможность деления с остатком m на n для любого целого m и целого , доказывается индукцией по m.

Проще сформулировать алгоритм Евклида так: если даны натуральные числа a и b и, пока получается положительное число, по очереди вычитать из большего меньшее, то в результате получится НОД.

Бинарный алгоритм

Бинарный алгоритм Евклида — метод нахождения наибольшего общего делителя двух целых чисел, основанный на использовании следующих свойств НОД:

· НОД(2m, 2n) = 2 НОД(m, n),

· НОД(2m, 2n+1) = НОД(m, 2n+1),

· НОД(-m, n) = НОД(m, n)

Алгоритм

· НОД(0, n) = n; НОД(m, 0) = m; НОД(m, m) = m;

· НОД(1, n) = 1; НОД(m, 1) = 1;

· Если m, n чётные, то НОД(m, n) = 2*НОД(m/2, n/2);

· Если m чётное, n нечётное, то НОД(m, n) = НОД(m/2, n);

· Если n чётное, m нечётное, то НОД(m, n) = НОД(m, n/2);

· Если m, n нечётные, то НОД(m, n) = НОД(n, |m - n|).