2020-01-14
109
Постановка математической задачи
Сформулируем математическую модель.
Целевая функция: 
Формула универсальна и позволяет рассчитать значение конкурентоспособности для любой фирмы s из всех фирм, представленных на рынке (общее число фирм – r).
Нам необходимо увеличить коэффициент конкурентоспособности. Возможно, не удастся найти его максимальное значение, но наша задача сделать его как можно больше.
Распишем подробнее основные переменные целевой функции:
, 
;
, 
, 
;
, 
.
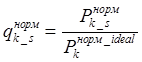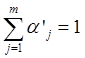Управляемыми переменными являются: 
, 
, 
.
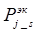Ограничения:
, 
;
, 
, 
.
Дополнительное условие:
Функция 
показывает каково будет распределение средств (у. е.) по различным параметрам 
, , 
:
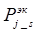– для улучшения технических характеристик 
;
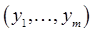– для понижения экономических параметров 
;
– для достижения требуемых норм 
.
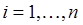-число технических характеристик,
- число экономических характеристик,
- число нормативных параметров,
– общее число фирм на рынке.
Классификация задачи
Классифицируем поставленную математическую модель.
Практические задачи оптимизации, которые сводятся к математическим моделям вида: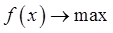 
, 
, где множество допустимых значений определяется ограничениями-равенствами или ограничениями-неравенствами 
или 
, при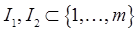 
-заданному множеству индексов, то они называются задачами математического программирования.
Если функции 
и 
- нелинейные и все управляемые переменные неотрицательны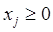 
, то это задача нелинейного программирования. В нашей задаче существует особенность целевой функции – она является дробно-линейной функцией, а значит, мы рассматриваем задачу дробно-линейного программирования.
Такая задача сводится к задаче линейного программирования. Существует несколько наиболее часто используемых методов для решения задач линейного программирования, к ним относится графический метод, симплекс-таблица и различные разновидности симплекс-метода.
Графический метод неприменим из-за количества управляемых переменных, их слишком много. Допустимым множеством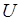 
будет являться многогранник в 
мерном пространстве. Основная черта – наглядность – теряется.
Затруднения использования симплекс-метода связанны не только с той же проблемой, что у графического метода, к ней еще прибавляется сложность приведения к каноническому виду, представления в симплекс-таблицах.
Изменение управляемых переменных задано дискретным рядом значений, а значит, можем классифицировать поставленную задачу, как дискретную задачу оптимизации.
Часто применимый для таких задач метод ветвей и границ.
