Неподвижные точки аффинных преобразований

Найдём координаты неподвижных точек аффинного преобразования (2). Для неподвижных точек, то есть для точек, переходящих в себя при аффинном преобразовании, должно выполняться следующее условие: z’=z, то есть

. (7)

Выразим отсюда z. Для этого решим следующую систему

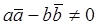(где ) (8)

Получили координату точки, являющейся инвариантом аффинного преобразования с коэффициентами a, b, c.

Тогда для аффинного преобразования возможны три случая [1]:

1) неподвижных точек не существует;

2) неподвижная точка единственная;

3) неподвижных точек бесконечно много.

Рассмотрим каждый из этих случаев.

1. Неподвижных точек не существует тогда и только тогда, когда для коэффициентов преобразования выполняется условие: 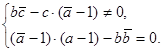Преобразовав второе условие системы, получим . (9)

Выполнимость этой системы и является условием того, что для данного аффинного преобразования неподвижных точек не существует.

2. Неподвижная точка единственна тогда и только тогда, когда

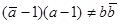, то есть 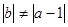(10)

3. Неподвижных точек бесконечно много тогда и только тогда, когда выполняется условие что равносильно системе

(11)

Возьмём условие неподвижности точки: (12)

и рассмотрим два случая:

1) Пусть с≠0, тогда умножим (12) на с, получим: . Воспользовавшись системой (11), получим равенство:

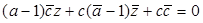, (13)

где коэффициенты при z и сопряжены, а свободный член является действительным числом, следовательно, равенство (13) при условии (11) задаёт прямую неподвижных точек.

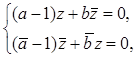2) Пусть теперь с=0, тогда (12) представится в виде . Выразим отсюда z: , откуда 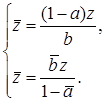Приравняем правые части и получим равенство , что равносильно условию . Поделим на z ≠0, в результате чего получим . То есть условие (11) задаёт прямую неподвижных точек (12), которая называется осью аффинного преобразования. Если такая прямая есть, то аффинное преобразование называется родством.