2020-01-14
918
Если на плоскости задана система координат, то одну из двух ориентаций плоских фигур называют обычно положительной, а другую – отрицательной. За положительную принимается ориентация, определяемая обходом координатного треугольника ОЕ1Е2 (рис. 1) или, что то же самое, направлением вращения от вектора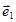 
к вектору 
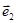(на угол, меньший 1800). В связи с этим введём также понятие ориентации пары векторов: будем называть пару векторов 
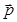и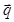 
ориентированной положительно, если направление вращения (на наименьший возможный угол) от 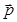к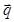 
совпадает с направлением вращения от 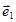к 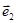; в противном случае пару векторов 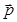и 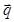назовём ориентированной отрицательно.
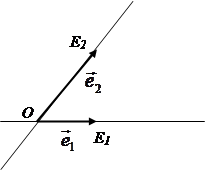
Рис. 1
Выясним теперь, как определить ориентацию пары векторов 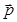и 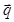, заданных своими комплексными координатами p и q соответственно. Очевидно, что если угол между векторами положительно ориентирован, то его синус положителен, в противном случае – отрицателен.
Используем формулу синуса угла между векторами, заданными своими комплексными координатами: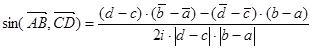 
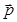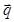. Найдём синус угла между векторами (p) и (q):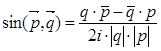 
. Здесь числитель – чисто мнимое число, следовательно, знак синуса угла зависит от знака числа 
.
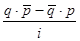Образом вектора 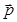(p) при аффинном преобразовании (2) будет вектор 
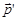с комплексной координатой 
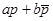, вектор 
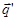, являющийся образом вектора 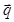(q) при этом же аффинном преобразовании будет иметь комплексную координату 
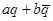. Найдём теперь синус угла между векторам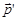и и :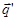 
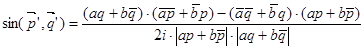. Упростив правую часть равенства, получим: 
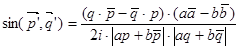. Знак синуса угла между векторам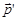и и 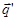зависит от знаков выражени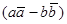й 
и 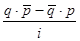так как второе из них присутствует в выражении 
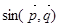, то именно от выражения 
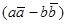зависит, будет ли знак синуса угла между векторам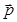и и 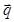отличаться от знак синуса угла между векторам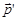и и 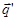. То есть если значение выражения 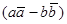положительно, то ориентация пары векторов 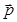и 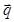будет совпадать с ориентацией пары векторов 
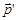и 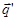. В противном случае при аффинном преобразовании (2) ориентация пары векторов сменится на противоположную.
Таким образом, аффинное преобразование (2) сохраняет ориентацию пары векторов (и, соответственно, плоских фигур) в случае, когда его определитель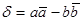 
положителен. В этом случае преобразование (2) является аффинным преобразованием первого рода. Иначе, аффинное преобразование меняет ориентацию пары векторов (и, соответственно, плоских фигур) в случае, когда его определитель отрицателен. И в таком случае преобразование (2) является аффинным преобразованием второго рода.
