Найдём собственные числа λ преобразования сжатия (24) из условия 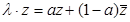 . Составим систему из этого условия и сопряжённого к нему выражения:
. Составим систему из этого условия и сопряжённого к нему выражения: 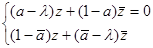 . Чтобы найти собственные числа, нужно решить уравнение
. Чтобы найти собственные числа, нужно решить уравнение 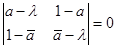 , откуда получим
, откуда получим 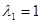 и
и 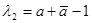 .
.
Примем без доказательства следующую теорему [1]: если λ – собственное действительное число аффинного преобразования, то множество точек, каждая из которых делит в отношении 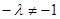 отрезок, соединяющий точку с её прообразом, есть двойная прямая этого преобразования.
отрезок, соединяющий точку с её прообразом, есть двойная прямая этого преобразования.
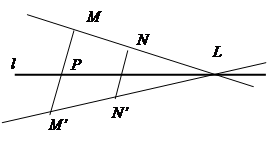 |
Рис. 3
Очевидно, что прямые MM’ и NN’ (рис. 3) являются двойными прямыми и λ2 – действительное число, то точка Р делит отрезок MM’ в отношении 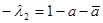 , то есть
, то есть 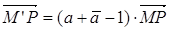 . Число
. Число 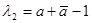 = δ называется коэффициентом сжатия. Если а – действительное число, то направление сжатия перпендикулярно его оси и сжатие называется прямым (ортогональным) сжатием.
= δ называется коэффициентом сжатия. Если а – действительное число, то направление сжатия перпендикулярно его оси и сжатие называется прямым (ортогональным) сжатием.
Рассмотрим частный случай сжатия – косую симметрию [1]. Это инволютивное преобразование, то есть оно тождественно преобразованию, обратному ему. Преобразование, обратное (24), имеет формулу:
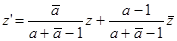 (25)
(25)
Оно имеет ту же ось, что и (24). Равенство преобразований (24) и (25) имеет место тогда и только тогда, когда 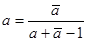 , откуда
, откуда 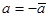 , то есть а – чисто мнимое число. Таким образом, формулой (24) при условии
, то есть а – чисто мнимое число. Таким образом, формулой (24) при условии 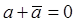 задаётся косая симметрия с действительной осью. В этом случае коэффициент сжатия равен
задаётся косая симметрия с действительной осью. В этом случае коэффициент сжатия равен 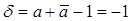 , следовательно, ось косой симметрии делит пополам каждый отрезок, соединяющий соответственные точки. Косая симметрия – аффинное преобразование второго рода, так как его определитель отрицателен.
, следовательно, ось косой симметрии делит пополам каждый отрезок, соединяющий соответственные точки. Косая симметрия – аффинное преобразование второго рода, так как его определитель отрицателен.
Если а=0, получаем осевую симметрию относительно действительной оси. Осевая симметрия – аффинное преобразование также второго рода (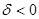 ).
).
Сдвиг
Выясним, как перемещается по плоскости точка при сдвиге (рис.4). Рассмотрим равенство (22), возьмём модули обеих частей этого равенства
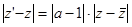 (26)
(26)
и посмотрим, чем является каждый модуль в (26).
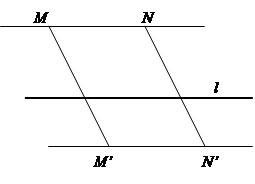 |
Рис. 4
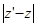 - это расстояние от точки М(z) до её образа M’(z’) при аффинном преобразовании.
- это расстояние от точки М(z) до её образа M’(z’) при аффинном преобразовании. 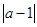 - это модуль постоянного вектора, перпендикулярного направлению сдвига, а
- это модуль постоянного вектора, перпендикулярного направлению сдвига, а 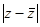 - это расстояние от М(z) до точки с координатой, сопряжённой z, равное удвоенному расстоянию от точки M(z) до действительной оси Ох.
- это расстояние от М(z) до точки с координатой, сопряжённой z, равное удвоенному расстоянию от точки M(z) до действительной оси Ох.
Преобразуем правую часть (26): 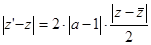 , (27) тогда из (22) и (27) следует, что при сдвиге каждая точка M(z) смещается параллельно его оси на расстояние
, (27) тогда из (22) и (27) следует, что при сдвиге каждая точка M(z) смещается параллельно его оси на расстояние 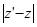 , пропорциональное расстоянию
, пропорциональное расстоянию 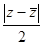 от этой точки до действительной оси. Коэффициент пропорциональности этих расстояний
от этой точки до действительной оси. Коэффициент пропорциональности этих расстояний 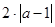 называется коэффициентом сдвига.
называется коэффициентом сдвига.
Найдём собственные числа преобразования сдвига из уравнения, составленного аналогично тому, как составляли для сжатия: 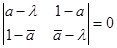 , откуда найдём
, откуда найдём 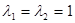 . Значит, преобразование сдвига имеет только один инвариантный пучок параллельных прямых, параллельных оси сдвига.
. Значит, преобразование сдвига имеет только один инвариантный пучок параллельных прямых, параллельных оси сдвига.
Определитель преобразования сдвига 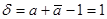 строго больше нуля, поэтому сдвиг – аффинное преобразование первого рода.
строго больше нуля, поэтому сдвиг – аффинное преобразование первого рода.
 2020-01-14
2020-01-14 170
170








