Эллиптический поворот

Эллипс – это образ окружности при аффинном преобразовании. [1]

Рассмотрим  ортогональное  сжатие g  к действительной  оси.

 

Его задают условия: 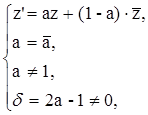                                                                              (28)                                                                                        

а обратное к нему аффинное преобразование g^-1 имеет формулу: , где 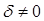, откуда в силу (28) обратное преобразование имеет вид:  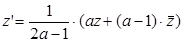                                                                                      (29)

При ортогональном сжатии окружность 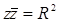перейдёт в эллипс (рис. 5). Коэффициент рассматриваемого сжатия равен 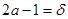, тогда 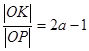.  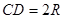и 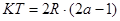 называются большой и малой осями эллипса при 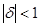. Найдём уравнение этого эллипса. Для этого в уравнении окружности заменим z на правую часть (29), получим: 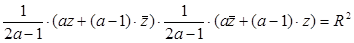, тогда 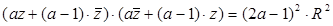. Преобразовав данное равенство, получим: 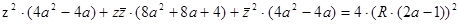, откуда получаем уравнение эллипса .

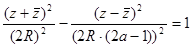Рассмотрим две произвольные точки окружности N и N₁. Точку N можно перевести в точку N₁ поворотом h на некоторый угол 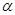 вокруг точки О: 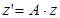, где , , .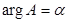

 

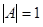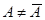                                                   Y

                                            P       N₁

                                                                    N

                                                                    M                                             

                                            K          M₁

 

 

                C                     O                           D                           X

 

                                            Т

                                            

 

                                            Q

                                            

                                             Рис. 5

 

Пусть точки М и М₁ – образы точек соответственно N и N₁ при ортогональном сжатии g. Тогда точку М можем перевести в точку М₁ следующим образом:

1)  (преобразование, обратное ортогональному сжатию);

2) 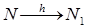 (поворот вокруг точки О на угол );

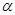3) 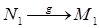 (ортогональное сжатие).

Тогда , где . Найдём формулу преобразования f.

1. Сначала найдём формулу преобразования : .

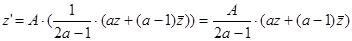2. Найдём формулу для преобразования f: 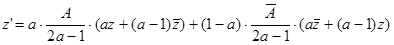, откуда получаем  - это формула эллиптического поворота.

Проверим, будет ли определитель рассматриваемого преобразования не равен нулю. Преобразуем выражение определителя

, используя равенство 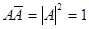, тогда получим, что . Следовательно, определитель преобразования не равен нулю, и f является аффинным преобразованием, что и требовалось доказать.

Так как определитель рассматриваемого аффинного преобразования положителен, то эллиптический поворот – это аффинное преобразование первого рода.

Это преобразование имеет единственную неподвижную точку О, значит оно является центроаффинным. При этом преобразовании каждая точка М плоскости (М ≠ О) переходит в другую точку, которая принадлежит соответствующему эллипсу. Этот эллипс при рассмотренном преобразовании переходит сам в себя. Преобразование с объявленными свойствами называется эллиптическим поворотом.

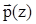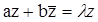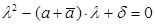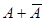Выясним, имеет ли эллиптический поворот инвариантные пучки параллельных прямых. Для этого найдём дискриминант характеристического уравнения этого преобразования. Комплексные координаты векторов  при аффинном преобразовании (2) переходят в коллинеарные им векторы  по формуле , откуда получаем уравнение . Решая его, получим характеристическое уравнение . Найдём (), его значение равно , тогда характеристическое уравнение запишется в виде: 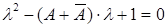. Его дискриминант  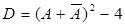отрицателен (так как 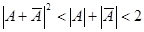). Следовательно, f – аффинное преобразование с единственной неподвижной точкой О и не имеющее инвариантных пучков параллельных прямых, то есть эллиптический поворот – эквицентроаффинное преобразование.

Формулу (29) эллиптического поворота можно записать в виде системы условий: 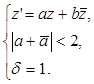   Эту формулу можно представить иначе: , то есть эллиптический поворот является композицией сжатия к действительной оси 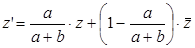 и подобия первого рода  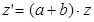с центром в точке О.

 

 §4. Параболический поворот

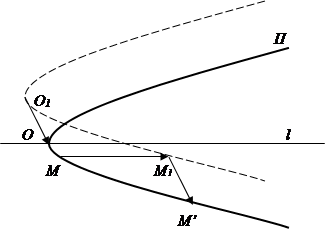
Покажем, что параболу можно перевести в себя при преобразовании её с помощью композиции сдвига и параллельного переноса, не параллельного оси сдвига. Пусть М – произвольная точка параболы П с осью l (рис. 6), примем эту ось за действительную. Произведём сдвиг с этой же осью l: 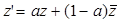, где 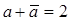,  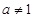. Этот сдвиг переведёт точку М в точку М₁ и параболу П – в параболу П₁. Параболы П и П₁ равны с точностью до сдвига.

 

	П1

 

 

                     

                                                            Рис. 6

 

Теперь произведём параллельный перенос параболы П₁: 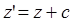(), где 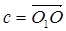. Тем самым, парабола П ₁ перейдёт в параболу П, а точка М₁ перейдёт в точку М’ параболы П.

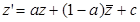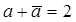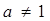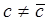Таким образом получили, что парабола переходит в себя при преобразовании её с помощью композиции сдвига и параллельного переноса, не параллельного оси сдвига [1,3]. Это преобразование называется параболическим поворотом и имеет формулу  , где , ,                               (30)                                  

Определитель найденного преобразования 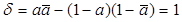. Так как определитель отличен от нуля, параболический поворот является аффинным преобразованием, а так как он больше нуля, - аффинным преобразованием первого рода.

Найдём собственные числа параболического поворота аналогично тому, как делали это для других рассмотренных аффинных преобразований. Найдём собственные числа λ из условия 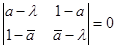. В процессе нахождения приходим к характеристическому уравнению 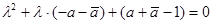, но так как 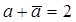, характеристическое уравнение примет вид 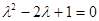, откуда 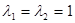. Следовательно параболический поворот имеет только один инвариантный пучок параллельных прямых, параллельных оси сдвига.