Элементарные высказывания в логике высказывания рассматриваются как не расчленяемые "атомы", а составные высказывания - как "молекулы'', образованные из "атомов" применением к ним логических операций. Логика высказываний интересуется единственным свойством элементарных высказываний их значением истинности, составные же высказывания изучаются ею со стороны их структуры, отражающей способ, которым они образованы. Структура составных высказываний определяет зависимость их значений истинности от значений истинности составляющих элементарных высказываний.
Пусть А, В, С и т.д. - переменные, вместо которых можно подставлять любые элементарные высказывания с помощью этих переменных и символов логики любое высказывание можно формализовать, то есть заменить формулой выражающей ее логическую структуру.
Например, высказывание: "Если 20 делится на 2 и на 5, то 20 делится на 10", формализуется в виде 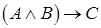 . Такая же формула соответствует предложению: "если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник - параллелограмм "
. Такая же формула соответствует предложению: "если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник - параллелограмм "
Уточним понятие формулы логики высказываний. Для этого сначала зададим алфавит, то есть набор символов, которые можно употреблять в логике высказываний.
1) А,В,С и т.д. - символы для обозначения высказываний;
2) 1 и 0 - символы, обозначающие логические константы "истина", «ложь»;
3) 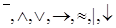 - символы, логические операции;
- символы, логические операции;
4) (,) - скобки, вспомогательные символы, служащие для указания порядка выполнения операций.
Дадим строгое определение формулы логики высказываний.
1) Всякое высказывание – это формула;
2) Символы 1, 0 – формулы;
3) Если А - формула, то 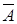 - тоже формула;
- тоже формула;
4) Если А1 и А2 - формулы, то
5) 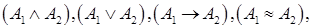
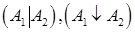 - формулы;
- формулы;
6) Никаких других формул в логике высказываний нет.
Алгоритм формализации высказывания
1) Простые высказывания заменяем переменными;
2) Логические связки заменяем соответствующими символами;
3) Расставляем вспомогательные символы, скобки: (,) в соответствии со смыслом данного высказывания.
Формула алгебры высказываний принимает одно из двух значений (0 или 1) в зависимости от простых высказываний и от связи между ними.
Истинность или ложность высказывания мы будем задавать таблицей истинности.
Составление истинностных таблиц происходит по следующему правилу:
Сначала необходимо записать всевозможные наборы высказываний, при этом каждое из высказываний может войти в одном из двух состояний (0 или 1). Далее, последовательно, в соответствии с порядком выполнения логических операций, под каждой логической операцией следует записывать истинные значения. Обратите внимание, если формула содержит п высказываний, то таблица истинности будет содержать 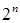 строк.
строк.
При составлении таблиц необходимо следить за тем, чтобы не перепутать порядок действий. Заполняя таблицу, следует двигаться "изнутри наружу", то есть от элементарных формул к более и более сложным. Столбец, заполняемый последним, содержит значения исходной формулы /4/.
Порядок выполнения операций определяется с помощью скобок. В отсутствии скобок первой выполняется операция отрицание, затем конъюнкция, после этого дизъюнкция, далее в порядке следования импликация, эквиваленция и т.д.
Пример 1:
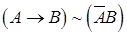
| А | В | 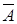 | 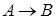 | 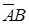 | 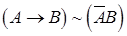 |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 |
Пример 2: Вычислить значение функции:
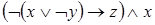 при
при 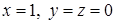
1) 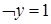
2) 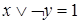
3) 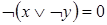
4) 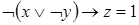
5) 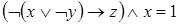
Подобно алгебраическим выражениям большие составные логические формулы во многих случаях могут быть упрощены, то есть приведены к равносильным.
Две формулы А и В будем называть равносильными (А=В или 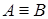 ), если они имеют одинаковые таблицы истинности. Будем считать две таблицы истинности одинаковыми, если у них одинаковые последние (результирующие) столбцы.
), если они имеют одинаковые таблицы истинности. Будем считать две таблицы истинности одинаковыми, если у них одинаковые последние (результирующие) столбцы.
Пример:
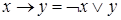
| x | y | 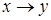 | 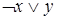 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
В логике высказываний будем считать, что равносильные формулы задают одно и то же высказывание. Может оказаться, что в последнем столбце таблицы истинности стоят одни единицы или нули. Будем называть такое высказывание тождественно-истинным (тавтологией) соответственно тождественно-ложным (противоречием) и обозначать 1 и 0. Из определения следует, что для проверки равносильности формул нужно построить их таблицы истинности и сравнить
Пример:
Формулы 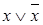 и
и 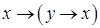 являются тождественно-истинными
являются тождественно-истинными
| х | у | 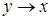 | 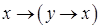 | |||
| 1 | 1 | 1 | 1 | |||
| 1 | 0 | 1 | 1 | |||
| 0 | 1 | 0 | 1 | |||
| 0 | 0 | 1 | 1 | |||
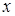 |
|
| ||||
| 1 | 0 | 1 | ||||
| 1 | 0 | 1 | ||||
| 0 | 1 | 1 | ||||
| 0 | 1 | 1 | ||||
Для упрощения логических высказываний могут быть использованы следующие равносильности (свойства):
Свойства конъюнкции и дизъюнкции
1. Коммутативные (переместительные) законы
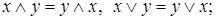
2. Ассоциативные (сочетательные) законы
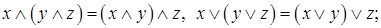
3. Дистрибутивные (распределительные) законы
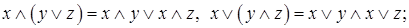
4. Законы поглощения
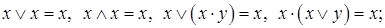
5. Законы склеивания
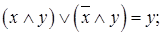
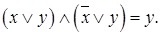
Свойства с отрицанием
1. Законы Де Моргана 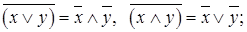
3. Закон противоречия 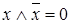 ;
;
4. Закон исключения третьего 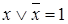 .
.
Свойства с логическими константами
1. 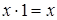 ,
, 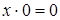 ;
;
2. 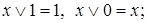
3. 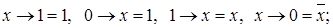
4. 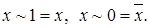
Связь между логическими операциями
1. 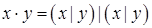 ;
;
2. 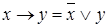 ,
, 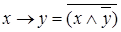 ;
;
3. 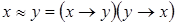 ,
, 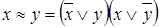 ;
;
4. 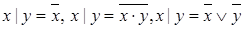 ;
;
5. 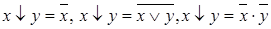
 2020-01-14
2020-01-14 1087
1087

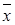
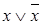
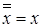 ;
;






