2020-01-14
128
Если 
есть дробно-рациональная функция, причем степень числителя A (p) меньше степени знаменателя B (p), то эту дробь разлагают на сумму простых дробей и находят оригиналы для каждой простой дроби либо непосредственно по формуле (1), либо по таблице (см. приложение).
Пример 1. Найти оригинал по изображению.
Разложим функцию на сумму дробей:
Найдем методом неопределенных коэффициэнтов А, В, С:
Тогда
Воспользуемся приложением:
В итоге оригинал равен
Первая теорема разложения
Теорема. Если изображение искомой функции может быть разложено в степенной ряд по степеням 
, т.е.
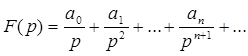
(причем этот ряд сходится к F (p) при 
), то оригинал имеет вид
(причем ряд сходится при всех значениях t).
Решение задачи Коши для обыкновенных линейных
Дифференциальных уравнений с постоянными коэффициентами
Рассмотрим линейное дифференциальное уравнение
где ak –действительные числа.
Требуется найти решение данного дифференциального уравнения, удовлетворяющее начальным условиям
x(0)=x0, x`(0)=x`0, …, x(n-1)(0)=x0(n-1)
где x0, x`0, …, x0(n-1) – заданные числа.
Будем предполагать, что искомая функция x (t), все ее производные, а также функция f (t) являются оригиналами.
Пусть 
. По формулам дифференцирования оригиналов
Перейдем от данного дифференциального уравнения к уравнению в изображениях
Перепишем его так 
, где 
, а 
Находим так называемое операторное решение уравнения
Найдя оригинал x (t) по его изображению X (p), мы получим тем самым решение задачи Коши для исходного дифференциального уравнения.
Примеры
Пример 1.
Найти решение дифференциального уравнения x (t)4 x (t)5 x (t),
удовлетворяющее условиям x (0) , x () 1.
Решение. Запишем уравнение в изображениях
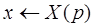
Вынесем Х за скобки
Найдем оригинал используя выведенные ранее значения в таблице приложения:
искомое решение - 
Пример 2.
Решить дифференциальное уравнение y `-2 y =0, y (0)=1.
Решение
Пример 3.
Решить дифференциальное уравнение y `+ y = et, y (0)=0.
Решение
Перейдем к уравнению
Пример 4.
Найти решение уравнения 
при начальных условиях y (0)=-1, y `(0)=0.
Решение
Пусть 
, тогда 
, 
.
Тогда 
- изображающее уравнение. Отсюда
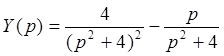
Оригинал для правого слагаемого известен 
, а оригинал для 
удобнее найти по теореме свертывания.
Известно, что 
, поэтому
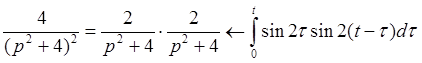
Так как 
, то
Таким образом,
Пример 5.
Найти общее решение уравнения 
.
Решение
Для получения общего решения начальные условия зададим так:
y( 0 )=C 1, y`( 0 ) = C 2
Если 
, то 
, 
.
И изображение уравнения имеет вид
Отсюда
Согласно приложению
,
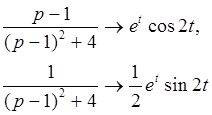
Собирая оригиналы всех слагаемых, представляющих Y (p), получаем искомое решение:
если 
.
Пример 6
Операционный метод может быть применён для решения нестационарных задач математической физики. Рассмотрим случай, когда некая функция u(x,t) зависит лишь от пространственной координаты x и времени t.
Для уравнения теплопроводности будем решать краевую задачу:
a 2= const, u (x,0)=φ(x) - начальные условия и u (0, t)=ψ1(t), u (l,t)=ψ2(t), 0 ≤ x ≤ l – краевые условия.
Пусть все функции являются оригинальными. Обозначим
- изображение по Лапласу.
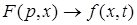
Тогда
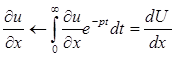
Тогда краевые условия:
Уравнение в изображениях:
