Если  , то
, то  , то есть интегрированию оригинала в пределах от 0 до t соответствует деление изображения на р.
, то есть интегрированию оригинала в пределах от 0 до t соответствует деление изображения на р.
Если f (t) принадлежит множеству оригиналов, то и  будет принадлежать множеству оригиналов.
будет принадлежать множеству оригиналов.
Пусть  и
и 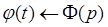 . Из
. Из  видно, что
видно, что
1) 
2)  .
.
Применим свойство дифференцирования оригинала к  , и в силу последних двух равенств получим
, и в силу последних двух равенств получим
 ,
,
А отсюда 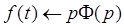 .
.
Но, по условию теоремы,  . Следовательно,
. Следовательно,  или
или  .
.
А отсюда и из соотношений 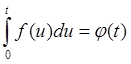 и
и  следует, что
следует, что  .
.
Интегрирование изображения
Если  и
и  принадлежит множеству оригиналов, то
принадлежит множеству оригиналов, то 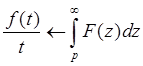 .
.
Изображения простейших функций
Единичная функция Хевисайда.
Имеем:
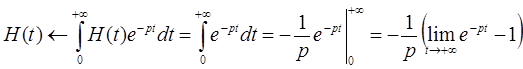
Так как при 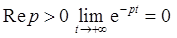 , то
, то  .
.
Для функции Хевисайда с запаздывающим аргументом  по теореме запаздывания получим
по теореме запаздывания получим
 .
.
Экспонента. По теореме смещения
 .
.
Гиперболические и тригонометрические функции.
В силу линейности преобразования Лапласа имеем
 ;
;
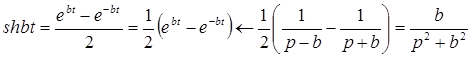 ;
;
 ;
;
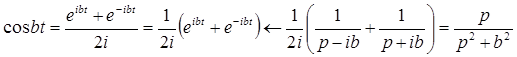
Степенная функция с натуральным показателем.
Положим  , где
, где  . Тогда при
. Тогда при 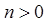
 .
.
При  , поэтому
, поэтому
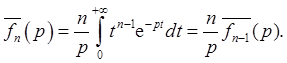
Отсюда
 .
.
Так как  , то
, то

Полученные с помощью формулы (1) изображения некоторых функций сведены в таблицу (см. приложение). Ее можно использовать для нахождения изображений функций.
Отыскание оригинала по изображению
Для нахождения оригинала f(t) по известному изображению F(p) нужно использовать формулы обращения Римана-Меллина
 .
.
Если функция f(t) является оригиналом, т.е. удовлетворяет условиям 1-3 определения 1 и F(p) служит ее изображением, то в любой точке своей непрерывности функция f(t) равна:

Формула обращения Римана-Меллина дает выражение оригинала f(t) через изображение F(p), причем α – произвольное число, удовлетворяющее неравенству α>s0.
Вычисление оригинала по формуле Римана-Меллина довольно трудоёмко, поэтому на практике при решении задач применяют другие методы, которые рассматриваются ниже.
 2020-01-14
2020-01-14 186
186








