Як ми вже відзначали, усе алгебри вважаються приналежними деякому фіксованому мальцевскому різноманіттю й використовуються стандартні позначення й визначення з[1].
Нагадаємо, що для 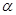 й
й  – конгруенції на алгебрі
– конгруенції на алгебрі  – говорять, що
– говорять, що  централізує
централізує 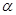 (записується:
(записується: 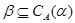 ), якщо на
), якщо на 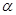 існує така конгруенція
існує така конгруенція  , що:
, що:
1) із  завжди треба
завжди треба
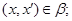
2) для будь-якого елемента 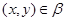 завжди виконується
завжди виконується

3) якщо 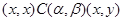 , те
, те
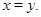
Очевидно, що для будь-якої конгруенції 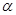 на алгебрі
на алгебрі  конгруенція
конгруенція 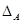 централізує
централізує 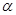 . У цьому випадку
. У цьому випадку  .
.
Помітимо, що якщо 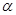 й
й  – конгруенції на групі
– конгруенції на групі  й
й 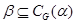 , те для нормальних підгруп
, те для нормальних підгруп  і
і  групи
групи  й будь-яких елементів
й будь-яких елементів  ,
,  мають місце наступні співвідношення:
мають місце наступні співвідношення:

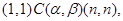

Тоді

і в силу транзитивності  із цих співвідношень треба, що
із цих співвідношень треба, що

По визначенню 2.1 одержуємо, що

Наступне визначення центральності належить Сміту.
Визначення 3.1. 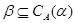 , якщо існує така
, якщо існує така  , що для будь-якого
, що для будь-якого 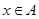 ,
,

Доведемо, що визначення 2.1. еквівалентно визначенню 3.1.  означає умову 1) з визначення 2.1. И навпаки, умова 1) означає, що
означає умову 1) з визначення 2.1. И навпаки, умова 1) означає, що 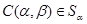 .
.
Нехай 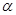 і
і  – конгруенції, що задовольняють визначенню 2.1. З умови 2) треба, що для будь-якого елемента
– конгруенції, що задовольняють визначенню 2.1. З умови 2) треба, що для будь-якого елемента 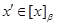 ,
,
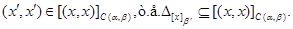
Доведемо зворотне включення.
Нехай  . Тому що
. Тому що 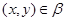 , те з умови 2) треба, що
, те з умови 2) треба, що
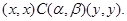
У силу транзитивності  маємо
маємо

і, виходить, у силу умови 3)  . Отже
. Отже

Покажемо, що з визначення 3.1. випливають умови 2) і 3) визначення 2.1. Якщо  , те
, те
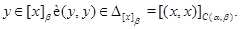
Це означає  .
.
Для 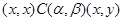 одержуємо, що
одержуємо, що

звідки 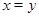 .
.
Відповідно до роботи
Визначення 3.2. Алгебра 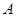 називається нильпотентною, якщо існує такий ряд конгруенції
називається нильпотентною, якщо існує такий ряд конгруенції
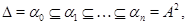
називаний центральним, що
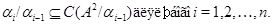
Лема 3.1. Будь-яка підалгебра нильпотентної алгебри нильпотентна.
Доказ:
Нехай  – підалгебра нильпотентной алгебри
– підалгебра нильпотентной алгебри 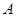 . Тому що
. Тому що  має центральний ряд
має центральний ряд

те для кожного 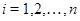 на алгебрі
на алгебрі  існує конгруенція
існує конгруенція  задовольняючому визначенню 2.1. А саме, з
задовольняючому визначенню 2.1. А саме, з

завжди треба

1) для будь-якого елемента

завжди виконується

2) якщо

и

те

Помітимо, що надалі, для скорочення запису, будемо враховувати той факт, що
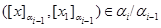
тоді й тільки тоді, коли

Побудуємо наступний ряд конгруенції на алгебрі  :
:
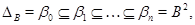
де

Покажемо, що цей ряд є центральним. Для цього на алгебрі 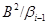 для кожного
для кожного  визначимо бінарне відношення
визначимо бінарне відношення  в такий спосіб:
в такий спосіб:

тоді й тільки тоді, коли
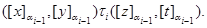
Покажемо, що  – конгруенція на алгебрі
– конгруенція на алгебрі  . Нехай
. Нехай

Тоді

і для кожної  -арної операції
-арної операції  маємо
маємо

Отже,

Отже,  – підалгебра алгебри
– підалгебра алгебри  .
.
Очевидно, що для будь-якого елемента  має місце
має місце

Таким чином, відповідно до леми 2.3,  – конгруенція на алгебрі
– конгруенція на алгебрі 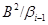 .
.
Нехай

Тоді  й тому що
й тому що 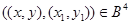 ,
,
те

Якщо  , то
, то  й, виходить,
й, виходить,

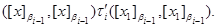
Нехай, нарешті,
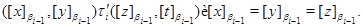
Тоді

і тому що
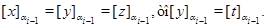
Отже,

Отже, конгруенція  задовольняє визначенню 2.1. для кожного
задовольняє визначенню 2.1. для кожного 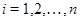 . Лема доведена.
. Лема доведена.
Лема 3.2. Нехай 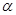 і
і  – конгруенції на алгебрі
– конгруенції на алгебрі 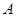 ,
,

і 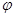 – ізоморфізм, певний на алгебрі
– ізоморфізм, певний на алгебрі 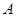 .
.
Тоді для будь-якого елемента  відображення
відображення
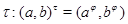
визначає ізоморфізм алгебри  на алгебру
на алгебру  , при якому
, при якому

Доказ:
Очевидно, що  – ізоморфізм алгебри
– ізоморфізм алгебри  на алгебру
на алгебру  , при якому конгруенції
, при якому конгруенції  й
й 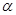 ізоморфні відповідно конгруенціям
ізоморфні відповідно конгруенціям 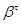 і
і  .
.
Тому що  , те існує конгруенція
, те існує конгруенція  на алгебрі
на алгебрі  , що задовольняє визначенню 2.1. Ізоморфізм
, що задовольняє визначенню 2.1. Ізоморфізм  алебри
алебри 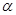 на алгебру
на алгебру  індуцирує у свою чергу ізоморфізм
індуцирує у свою чергу ізоморфізм 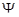 алгебри
алгебри  на алгебру
на алгебру  такий, що
такий, що

для будь-яких елементів  ,
,  .
.
Але тоді легко перевірити, що  – конгруенція на алгебрі
– конгруенція на алгебрі  ізоморфна конгруенції
ізоморфна конгруенції  . Це й означає, що
. Це й означає, що

Лема доведена.
Лема 3.3. Фактор-Алгебра нильпотентной алгебри нильпотентна.
Доказ:
Нехай
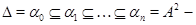
центральний ряд алгебри  . Покажемо, що для будь-якої конгруенції
. Покажемо, що для будь-якої конгруенції  на алгебрі
на алгебрі  ряд
ряд

є центральним, тобто
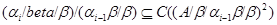
для кожного  . У силу відомих теорем про ізоморфизмах для алгебр (див., наприклад, теореми II.3.7, II.3.11) і леми 3.2., досить показати, що
. У силу відомих теорем про ізоморфизмах для алгебр (див., наприклад, теореми II.3.7, II.3.11) і леми 3.2., досить показати, що
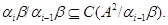
Нехай 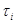 – конгруенція на алгебрі
– конгруенція на алгебрі  , що задовольняє визначенню 2.1. Визначимо бінарне відношення
, що задовольняє визначенню 2.1. Визначимо бінарне відношення  на алгебрі
на алгебрі 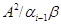 в такий спосіб
в такий спосіб

тоді й тільки тоді, коли найдуться такі елементи  , що
, що
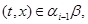

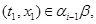


Безпосередньою перевіркою переконуємося, що  – конгруенція на алгебрі
– конгруенція на алгебрі 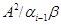 .
.
У такий спосіб залишилося показати, що  задовольняє визначенню 2.1.
задовольняє визначенню 2.1.
Нехай

тоді зі співвідношення
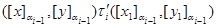
треба, що
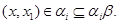
Тому що

те  . Отже,
. Отже,

Нехай  . Тоді для деякого елемента
. Тоді для деякого елемента  ,
, 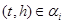 і
і  .
.
Таким чином,

отже,

Тому що  , те це означає, що
, те це означає, що

Нехай

де

Покажемо, що  . У силу визначення
. У силу визначення  найдуться
найдуться  , що
, що


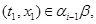


При цьому мають місце наступні співвідношення:


Отже,

Але тоді по визначенню 3.2.
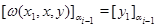
А тому що 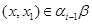 , те
, те

Тепер з того, що
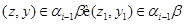
треба, що

Лема доведена.
Доказ наступного результату здійснюється простою перевіркою.
Лема 3.4. Нехай 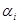 – конгруенція на алгебрі
– конгруенція на алгебрі  ,
, 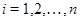 . Полога
. Полога

тоді й тільки тоді, коли  для кожного
для кожного  , одержуємо конгруенцію
, одержуємо конгруенцію  на алгебрі
на алгебрі 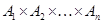 .
.
Лема 3.5. Прямий добуток кінцевого числа нильпотентних алгебр нильпотентне.
Доказ:
Очевидно, досить показати, що якщо 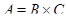 ,
,  і
і  – нильпотентне алгебри, те
– нильпотентне алгебри, те  – нильпотентна алгебра.
– нильпотентна алгебра.
Нехай


центральні ряди алгебр  і
і  відповідно. Якщо
відповідно. Якщо 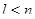 , те, ущільнивши перший ряд повторюваними членами, одержимо центральний ряд алгебри
, те, ущільнивши перший ряд повторюваними членами, одержимо центральний ряд алгебри  довжини
довжини 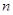 . Таким чином, можна вважати, що ці ряди мають однакову довжину, рівну
. Таким чином, можна вважати, що ці ряди мають однакову довжину, рівну 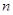 .
.
Побудуємо тепер ряд конгруенції на алгебрі  в такий спосіб:
в такий спосіб:

де 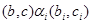 тоді й тільки тоді, коли
тоді й тільки тоді, коли  ,
, 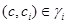 ,
,  .
.
Покажемо, що останній ряд є центральним, тобто 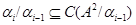 для довільного
для довільного 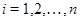 . Тому що
. Тому що

те на алгебрах 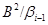 і
і  відповідно задані конгруенції
відповідно задані конгруенції  й
й 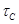 , що задовольняють визначенню 2.1.
, що задовольняють визначенню 2.1.
Визначимо бінарне відношення 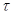 на алгебрі
на алгебрі  в такий спосіб:
в такий спосіб:
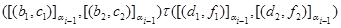
і тільки тоді, коли

и

Легко безпосередньою перевіркою переконатися, що  – конгруенція на алгебрі
– конгруенція на алгебрі 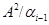 . Залишилося показати, що
. Залишилося показати, що  задовольняє визначенню 2.1.
задовольняє визначенню 2.1.
Нехай має місце
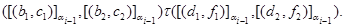
Тоді відповідно до уведеного визначення 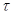

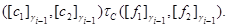
звідки треба, що
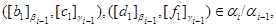
т.е.

Нехай

Це означає

Але тоді
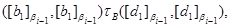
и

Отже,

Нехай має місце

Це означає, що

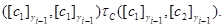
Виходить,  і
і  , тобто
, тобто  . Лема, доведена.
. Лема, доведена.
Як відомо, спадкоємною формацією називається клас алгебр, замкнутих відносно фактор-алгебр, підпрямих добутків і відносно підалгебр.
Результати, отримані в лемах 3.1, 3.3, 3.5 можна сформулювати у вигляді наступної теореми.
Теорема 7 Клас всіх нильпотентних алгебр мальцевського різноманіття є спадкоємною формацією.
Визначення 3.3.  -арна група
-арна група  називається нильпотентной, якщо вона має такий нормальний ряд
називається нильпотентной, якщо вона має такий нормальний ряд
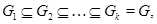
що

и

для кожного 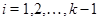 .
.
Тому що конгруенції на 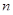 -арних групах попарно перестановочні (дивися, наприклад,), те це дає можливість використовувати отримані результати в дослідженні таких груп.
-арних групах попарно перестановочні (дивися, наприклад,), те це дає можливість використовувати отримані результати в дослідженні таких груп.
Лема 3.6. Нехай  –
– 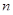 -арна група.
-арна група.  і
і  – нормальні підгрупи групи
– нормальні підгрупи групи 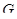 й
й  .
.
Тоді  , де
, де  й
й  конгруенції, індуковані відповідно підгрупами
конгруенції, індуковані відповідно підгрупами  й
й  на групі
на групі  .
.
Доказ:
Підгрупи  й
й  індуцирують на групі
індуцирують на групі  конгруенції
конгруенції  й
й  , обумовлені в такий спосіб:
, обумовлені в такий спосіб:
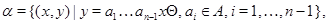

 –
–  -арна операція.
-арна операція.
Визначимо на  бінарне відношення
бінарне відношення 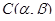 в такий спосіб:
в такий спосіб:

тоді й тільки тоді, коли існують такі послідовності елементів 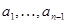 і
і 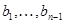 з
з  і
і  відповідно, що
відповідно, що



Покажемо, що 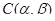 – підалгебра алгебри
– підалгебра алгебри 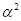 . Для скорочення запису будемо надалі опускати
. Для скорочення запису будемо надалі опускати  -арний оператор
-арний оператор  .
.
Нехай

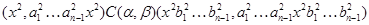
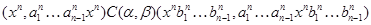
Тому що  , те
, те

Тому що  , те
, те

Тому в силу того, що  ,
,

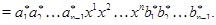
Отже,  – підалгебра алгебри
– підалгебра алгебри 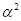 .
.
Нехай 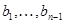 – нейтральна послідовність групи
– нейтральна послідовність групи  , а, отже, і групи
, а, отже, і групи  . Тоді з визначення бінарного відношення
. Тоді з визначення бінарного відношення 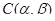 треба, що
треба, що

Тим самим довело, що  – конгруенція на
– конгруенція на  .
.
Тo, що  задовольняє визначенню 2.1, очевидно. Лема доведена.
задовольняє визначенню 2.1, очевидно. Лема доведена.
Лема 3.7. Нехай 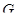 – нильпотентна
– нильпотентна  -арна група. Тоді
-арна група. Тоді  задовольняє визначенню 2.1.
задовольняє визначенню 2.1.
Доказ:
Тому що  для кожного
для кожного 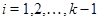 , те
, те  індуцирує конгруенцію
індуцирує конгруенцію  на
на 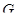 . У такий спосіб
. У такий спосіб  володіє поруч конгруенції, що у силу леми 3.6 буде центральним. Лема доведена.
володіє поруч конгруенції, що у силу леми 3.6 буде центральним. Лема доведена.
Зокрема, для довільної бінарної групи 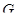 звідси треба, що
звідси треба, що  нильпотентна тоді й тільки тоді, коли,
нильпотентна тоді й тільки тоді, коли, 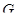 задовольняє визначенню 3.2. У цьому випадку теорема 3.2 просто констатує той факт, що клас всіх нильпотентних груп утворить спадкоємну формацію.
задовольняє визначенню 3.2. У цьому випадку теорема 3.2 просто констатує той факт, що клас всіх нильпотентних груп утворить спадкоємну формацію.
 2020-01-14
2020-01-14 93
93