Расчет геометрических размеров элементов

Структура проводников полосковых схем практически всегда многослойна, что позволяет добиться требуемой аргезии проводника к диэлектрическому основанию, достаточно малых потерь к высокой устойчивости к коррозии. Поэтому первый (от диэлектрического основания) слой проводника – высокоомный материал с хорошими оргезионными свойствами, второй слой – основной проводник – материал с высокой проводимостью, третий обеспечивает защиту от воздействия внешней среды и лужения всего проводника, либо его части, для проведения монтажных операций. В таблице 5.4 приведены характеристики материалов, используемые при изготовлении микро полосковых схем.

Сопротивление неэкранированной микро полосковой линии от трех параметров:

- - относительная диэлектрическая проницаемость материала на подложке;

- - толщина диэлектрической подложки, мм;

- - ширина проводника микро полосковой линии, мм;

Волновое сопротивление неэкранированной микро полосковой линии определяется выражением [5]:

, Ом (5.8)

Таблица 5.4 – Характеристики материалов

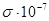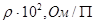
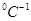
Металл	Относительное удельное сопротивление,	,Ом* м	См/м	Поверхностное сопротивление пленки	КТ-ЛР	ТКС,	Температура плавления,
Золото Никель Олово Хром Медь	0,941 4,01 6,62 7,6 1,0	0,0162 0,069 0,114 0,13 0,0172	6,6 1,28 0,90 0,77 5,9	2,7 13,0 - - 2,8	18,6 13,2 23,0 6,2 16,6	- 0,0047 0,0042 - 0,0039	961 1453 232 1900 1083

Микро полосковую линию конструктор варьируя параметрами и . Поэтому рабочие характеристики МПЛ, в том числе и ее волновое сопротивление (), определяется через соотношение . Выразим указанное соотношение через Х:

(5.9)

Подставим (5.9) в (5.8) м выразим Х:

Преобразуем полученное выражение:

(5.10)

Для решения уравнения (5.10) применяется метод Ньютона, который заключается в последовательном приближении к искомому значению корня с заданной точностью . Каждый последующий К+1 корень уравнения определяется выражением:

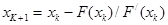
где - значение функции для предыдущего (к-го) значения корня;

- значение производной функции для предыдущего (к-го) значения корня;

, - предыдущее и последующее значение корня;

Для имеющейся зависимости:

Условие применимости корней является соотношение:

где - предел точности;

Исходные данные для расчета микро полосковой линии является:

- волновое сопротивление 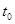, Ом=50;

- допуск , %=10;

- диэлектрическая проницаемость «Полинора», ;

- толщина подложки , мм=1;

- ;

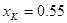Результаты расчета, согласно алгоритму, приведены на рисунке 5.1:

- при волновом сопротивлении 50 Ом отношение ;

- при волновом сопротивлении 55 Ом, отношение ();

- при волновом сопротивлении 45 Ом, отношение ();

- ширина полоска мм;

- допуск на мм;

Кольцевой делитель мощности состоит из двух четверть волновых отрезков линии передачи, две пары полюсов которых соединены параллельно, а две оставшиеся пары связаны через активное сопротивление.

Кольцевой делитель мощности обеспечивает разделение мощности поровну между двумя четверть волновыми отрезками. Также кольцевой делитель мощности обеспечивает суммирование мощностей СВЧ сигналов в плече, если к двум плечам подвести два синфазных сигнала.

При анализе работы кольцевого делителя мощности предполагается, что сопротивление является «точным». На практике длина участка включения сопротивления конечна и соизмерима с длиной волны в линии передачи. В этом случае для компенсации набега фазы на сопротивления кольцевой участок удлиняется на расчетную величину. Если длина участка включения сопротивления а сравнима с , то для компенсации набега фазы на этом участке необходимо удлинить кольцо на величину а, при этом длина кольцевого участка будет равна [6]:

(5.15)

Полная длина окружности определяется соотношением [6]:

(5.16)

где

(5.17)

(5.18)

При этом уравнение для вычисления радиуса кольца будет иметь вид [6]:

(5.19)

Уравнение (5.19) вида предполагается решать методом половинного деления интервала изоляции корня. Если найден интервал внутри которого содержится лишь один корень Х уравнения (5.19), то этот корень изолирован от других корней уравнения (5.19).

Дополнительное условие изоляции корня [6]:

- -непрерывна и дифференциальная на интервале ;

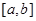- - знакопостоянна на интервале ;.

При выполнении этих условий существует только один корень V уравнения (5,19), принадлежащий интервалу 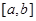. Задача сводится к тому, чтобы получить достаточно малый интервал изоляции корня Х.

Рисунок 5.2 - Блок – схема расчета

В методе половинного деления сужение интервала изоляции осуществляется по следующей процедуре. Находят точку:

(5.20)

где с – середина интервала .

Вычисляют и определяют знак произведения . Если 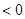, то в качестве нового интервала изоляции берут интервал , в противном случае будет интервал .

Описанную процедуру повторим применительно к уменьшенному интервалу до тех пор, пока длина уменьшаемого интервала не станет меньше некоторого числа 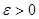, определяющую заданную границу погрешности.