$$$ 1
Тәуелсіз айнымалы, ізделініп отырған функция мен оның туындыларын байланыстырып тұратын қатынас:
A) Дифференциалдық теңдеулер.
$$$ 2
Егер дифференциалдық теңдеуде ізделініп отырған функция бір ғана айнымалыдан тәуелді болса, немесе, барлық туындылар бір айнымалыдан алынса, онда теңдеу:
B) Жай.
$$$ 3
Дифференциалдық теңдеудегі ізделініп отырған функцияның ең жоғарғы реті:
D) Дифференциалдық теңдеудің реті.
$$$ 4
Дифференциалдық теңдеудің шешімінің сүлбесі:
A) Интегралдық қисық.
$$$ 5
Егер  болса,
болса,  функциясы
функциясы  -ге тең болу керек шарты аталады:
-ге тең болу керек шарты аталады:
C) Бастапқы шарт.
$$$ 6
Бір кез келген  тұрақтысынан тәуелді және келесі шарттарды қанағаттандыратын теңдеу:
тұрақтысынан тәуелді және келесі шарттарды қанағаттандыратын теңдеу:
а)  шешімі
шешімі  болғанда дифференциалдық теңдеуді қанағаттандырады;
болғанда дифференциалдық теңдеуді қанағаттандырады;
б) бастапқы шарт  қандай болмасын,
қандай болмасын,  функциясы берілген бастапқы шартты қанағаттандыратындай
функциясы берілген бастапқы шартты қанағаттандыратындай  табу керек:
табу керек:
B) 1-ретті дифференциалдық теңдеудің жалпы шешімі.
$$$ 7
Дифференциалдық теңдеудің айқын түрде берілмеген жалпы шешімі:
C) Дифференциалдық теңдеудің жалпы интегралы.
$$$ 8
Белгілі бір  сандық мәнге ие болғанда дифференциалдық теңдеудің жалпы шешімінен алынған шешім:
сандық мәнге ие болғанда дифференциалдық теңдеудің жалпы шешімінен алынған шешім:
D) Дифференциалдық теңдеудің дербес шешімі.
$$$ 9
Кез келген тұрақтының нақты бір сандық мәнге ие болғанда, жалпы шешімнен алынбайтын шешімі:
E) Дифференциалдық теңдеудің ерекше шешімі.
$$$ 10
 жазықтығының
жазықтығының  дифференциалдық теңдеуінің шешіміне көлбеу жанама нүктелерінің геометриялық орны:
дифференциалдық теңдеуінің шешіміне көлбеу жанама нүктелерінің геометриялық орны:
B) Дифференциалдық теңдеудің изоклинасы.
$$$ 11
 дифференциалдық теңдеуінің изоклина теңдеуі:
дифференциалдық теңдеуінің изоклина теңдеуі:
D) 
 .
.
$$$ 12
Берілген  қисықтар үйірінің дифференциалдық теңдеулерін құру үшін, мұнда
қисықтар үйірінің дифференциалдық теңдеулерін құру үшін, мұнда  - үзіліссіз дербес туындысы бар, келесі теңдеулер жүйесінен
- үзіліссіз дербес туындысы бар, келесі теңдеулер жүйесінен  -ны тауып алу керек:
-ны тауып алу керек:
B) 
$$$ 13
 - дифференциалдық теңдеудің жалпы интегралы болсын. Дифференциалдық теңдеудің ерекше шешімін табу үшін келесі жүйеден
- дифференциалдық теңдеудің жалпы интегралы болсын. Дифференциалдық теңдеудің ерекше шешімін табу үшін келесі жүйеден  -ны табу керек:
-ны табу керек:
A) 
$$$ 14
 дифференциалдық теңдеудің түрі, мұнда
дифференциалдық теңдеудің түрі, мұнда  және
және  - берілген функциялар:
- берілген функциялар:
E) Айнымалысы бөліктенген дифференциалдық теңдеу.
$$$ 15
 мұнда
мұнда  - берілген функциялар, дифференциалдық теңдеуінің түрі:
- берілген функциялар, дифференциалдық теңдеуінің түрі:
C) Айнымалысы бөліктенетін дифференциалдық теңдеу.
$$$ 16
 мұнда
мұнда  - берілген функция,
- берілген функция,  теңдеуі айнымалысы бөліктенетін теңдеуге мына ауыстыру арқылы келтіріледі:
теңдеуі айнымалысы бөліктенетін теңдеуге мына ауыстыру арқылы келтіріледі:
C) 
$$$ 17
 теңдеуі, мұнда
теңдеуі, мұнда  -берілген функция, біртекті дифференциалдық теңдеу деп аталады, егер:
-берілген функция, біртекті дифференциалдық теңдеу деп аталады, егер:
D) 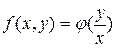 .
.
$$$ 18
 дифференциалдық теңдеуі, мұнда
дифференциалдық теңдеуі, мұнда  және
және  - берілген функциялар, біртекті дифференциалдық теңдеу деп аталады, егер:
- берілген функциялар, біртекті дифференциалдық теңдеу деп аталады, егер:
B)  ,
,  -
-  ,
,  қатысты бірдей өлшемді біртекті функциялар.
қатысты бірдей өлшемді біртекті функциялар.
$$$ 19
Белгісіз функцияға және оның туындысына қатысты сызықты болатын дифференциалдық теңдеу:
C) Сызықтық дифференциалдық теңдеу.
$$$ 20
 мұнда
мұнда 
 аралығында берілген функциялар, және
аралығында берілген функциялар, және  түріндегі дифференциалдық теңдеуі:
түріндегі дифференциалдық теңдеуі:
B) Регулярлы сызықтық дифференциалдық теңдеу.
$$$ 21
 мұнда
мұнда 
 аралығында берілген функциялар, және
аралығында берілген функциялар, және 
 аралығының кейбір нүктелерінде нөлге айналады, түріндегі дифференциалдық теңдеу:
аралығының кейбір нүктелерінде нөлге айналады, түріндегі дифференциалдық теңдеу:
C) Сингулярлы сызықтық дифференциалдық теңдеу.
$$$ 22
 мұнда
мұнда  және
және  -
-  аралығында берілген функциялар, және
аралығында берілген функциялар, және  түріндегі дифференциалдық теңдеуі:
түріндегі дифференциалдық теңдеуі:
E) Біртекті емес сызықтық дифференциалдық теңдеу.
$$$ 23
Бернулли  дифференциалдық теңдеуі сызықтық дифференциалдық теңдеуге келесі ауыстыру арқылы келеді:
дифференциалдық теңдеуі сызықтық дифференциалдық теңдеуге келесі ауыстыру арқылы келеді:
C)  .
.
$$$ 24
Риккати дифференциалдық теңдеуінің түрі:
B)  .
.
$$$ 25
Егер  теңдеуінің сол жағы, мұнда
теңдеуінің сол жағы, мұнда  және
және 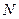 функцияларының берілген
функцияларының берілген 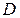 облысында үзіліссіз дербес туындылары бар болса, кейбір
облысында үзіліссіз дербес туындылары бар болса, кейбір  функциясының толық дифференциалы болса, онда дифференциалдық теңдеу:
функциясының толық дифференциалы болса, онда дифференциалдық теңдеу:
E) Толық дифференциалдық теңдеу.
$$$ 26
 дифференциалдық теңдеуі толық дифференциалдық теңдеу болу үшін қажетті және жеткілікті шарт:
дифференциалдық теңдеуі толық дифференциалдық теңдеу болу үшін қажетті және жеткілікті шарт:
D)  .
.
$$$ 27
 толық дифференциалдық теңдеуінің жалпы интегралы:
толық дифференциалдық теңдеуінің жалпы интегралы:
B)  где
где  .
.
$$$ 28
Дифференциалдық теңдеуге көбейткеннен кейін толық дифференциалдық теңдеуге айналатын функция:
E) Интегралдық көбейткіш.
$$$ 29
 айнымалысы бөліктенетін дифференциалдық теңдеудің
айнымалысы бөліктенетін дифференциалдық теңдеудің  интегралдық көбейткіші мына формуламен есептеледі:
интегралдық көбейткіші мына формуламен есептеледі:
D)  .
.
$$$ 30
 мұнда
мұнда  және
және  - берілген дифференциалданатын функциялар, түріндегі дифференциалдық теңдеу:
- берілген дифференциалданатын функциялар, түріндегі дифференциалдық теңдеу:
A) Лагранж дифференциалдық теңдеуі.
$$$ 31
 мұнда
мұнда  - берілген дифференциалданатын функция, дифференциалдық теңдеуі:
- берілген дифференциалданатын функция, дифференциалдық теңдеуі:
D) Клеро дифференциалдық теңдеуі.
$$$ 47
 теңдеуі:
теңдеуі:
C) Айнымалылары бөліктенетін теңдеу.
$$$ 48
 функциясы келесі дифференциалдық теңдеудің жалпы интегралы болып табылады:
функциясы келесі дифференциалдық теңдеудің жалпы интегралы болып табылады:
A)  .
.
F) 
H) 
$$$ 49
 теңдеуінің интегралдық көбейткіші:.
теңдеуінің интегралдық көбейткіші:.
E)  .
.
G) 
H) 
$$$ 50
 теңдеуі келесі ауыстыру арқылы интегралданады:
теңдеуі келесі ауыстыру арқылы интегралданады:
D)  - частное решение.
- частное решение.
$$$ 51
 теңдеуі келесі ауыстыру арқылы айнымалысы бөліктенетін теңдеуге келеді:
теңдеуі келесі ауыстыру арқылы айнымалысы бөліктенетін теңдеуге келеді:
C)  .
.
F)  .
.
H) 
$$$ 52
 теңдеуі келесі ауыстыру арқылы айнымалысы бөліктенетін теңдеуге келеді:
теңдеуі келесі ауыстыру арқылы айнымалысы бөліктенетін теңдеуге келеді:
E) 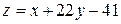 .
.
F) 
H) 
$$$ 53
 теңдеуі келесі ауыстыру арқылы айнымалысы бөліктенетін теңдеуге келеді:
теңдеуі келесі ауыстыру арқылы айнымалысы бөліктенетін теңдеуге келеді:
B)  , где
, где  .
.
F) 
H) 
$$$ 57
 дифференциалдық теңдеуі:
дифференциалдық теңдеуі:
D) Біртекті теңдеу.
$$$ 58
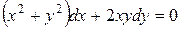 дифференциалдық теңдеуі:
дифференциалдық теңдеуі:
A) Біртекті теңдеу.
D) Толық дифференциалдық теңдеу.
$$$ 59
 дифференциалдық теңдеуі:
дифференциалдық теңдеуі:
A) Лагранж теңдеуі.
F) Туындысына қатысты айқындалмаған теңдеу.
G) Параметр енгізу арқылы шешілетін теңдеу.
$$$ 61
 дифференциалдық теңдеуі:
дифференциалдық теңдеуі:
E) Бернулли теңдеуі.
$$$ 65
 дифференциалдық теңдеуі:
дифференциалдық теңдеуі:
B) Біртекті емес сызықтық теңдеу.
F) Сызықтық теңдеу.
G) Бірінші ретті теңдеу.
$$$ 66
 дифференциалдық теңдеуі:
дифференциалдық теңдеуі:
A) Айнымалылары бөліктенетін теңдеу.
F) Бірінші ретті теңдеу.
G) Сызықтық емес теңдеу.
$$$ 68
Егер дифференциалдық теңдеудің жалпы интегралы  болса, онда ерекше шешім:
болса, онда ерекше шешім:
A)  .
.
F) 
G) 
$$$ 70
Егер дифференциалдық теңдеудің жалпы интегралы  болса, онда ерекше шешім:
болса, онда ерекше шешім:
A)  .
.
F) 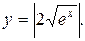
G) 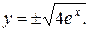
$$$ 71
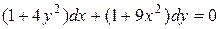 дифференциалдық теңдеуінің жалпы шешімі:
дифференциалдық теңдеуінің жалпы шешімі:
A)  .
.
F) 
$$$ 91
 біртекті емес дифференциалдық теңдеуінің дербес шешімі:
біртекті емес дифференциалдық теңдеуінің дербес шешімі:
F) 
G) 
$$$ 92
 Коши есебінің шешімі:
Коши есебінің шешімі:
B) 
C) 
$$$ 93
 Коши есебінің шешімі:
Коши есебінің шешімі:
B) 
C) 
$$$ 94
 Коши есебінің шешімі:
Коши есебінің шешімі:
B) 
C) 
$$$ 95
 Коши есебінің шешімі:
Коши есебінің шешімі:
B) 
C) 
$$$ 96
 дифференциалдық теңдеуінің жалпы шешімі:
дифференциалдық теңдеуінің жалпы шешімі:
B) 
C) 
$$$ 112
 теңдеуінің жалпы шешімі:
теңдеуінің жалпы шешімі:
A)  .
.
F) 
$$$ 149
 дифференциалдық теңдеуі, мұндағы
дифференциалдық теңдеуі, мұндағы  берілген функция,
берілген функция, 
 ;
;  келесі айнымалы ауыстыру арқылы интегралданады:
келесі айнымалы ауыстыру арқылы интегралданады:
A)  .
.
$$$ 155
 түрінде берілген теңдеудің ретін келесі түрде төмендетуге болады:
түрінде берілген теңдеудің ретін келесі түрде төмендетуге болады:
E) 
$$$ 156
 теңдеуі үшін интегралдаушы көбейткішті табыңыз
теңдеуі үшін интегралдаушы көбейткішті табыңыз
D) 
$$$ 157
 (
( ), (c1,c2
), (c1,c2  0)- теңдеуі қандай ауыстыру арқылы біртекті теңдеуге келтіріледі:
0)- теңдеуі қандай ауыстыру арқылы біртекті теңдеуге келтіріледі:
A) 
$$$ 158
Төмендегі ауыстыру арқылы теңдеу айнымалысы бөліктенетін теңдеуге келтіріледі:
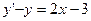 .
.
C) 
$$$ 159
Толық дифференциалдық теңдеуді көрсетіңіз:
D) 
$$$ 160
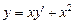 ,
,  түріндегі Коши есебінің шешімін көрсету керек:
түріндегі Коши есебінің шешімін көрсету керек:
E) 
$$$ 161
 теңдеуін шешіңіз:
теңдеуін шешіңіз:
C) 
$$$ 162
 теңдеуінің
теңдеуінің  бастапқы шарттарын қанағаттандыратын шешімін табу керек
бастапқы шарттарын қанағаттандыратын шешімін табу керек
B) 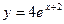
$$$ 163
Теңдеудің түрін анықтаңыз 
B) біртекті теңдеу
$$$ 164
Теңдеуге қандай ауыстыру жасайды 
C) 
$$$ 165
Бернулли теңдеуін қандай ауыстыру жасау арқылы сызықтық теңдеуге келтіруге болады:
E) 
$$$ 166
1-ретті сызықтық теңдеуді қандай әдіспен интегралдауға болады?
D) тұрақтыны вариациялау әдісі арқылы
$$$ 167
Риккати теңдеуінің  дербес шешімі белгілі болса, Бернулли теңдеуіне қалай келтіруге болады?
дербес шешімі белгілі болса, Бернулли теңдеуіне қалай келтіруге болады?
A) 
$$$ 169
Біртекті теңдеудің шешімін табыңыз: 
A) 
$$$ 170
Риккати теңдеуін көрсетіңіз:
B) 
$$$ 171
Туындысы бойынша айқындалмаған теңдеуді көрсетіңіз:
C) Клеро теңдеуі
$$$ 172
Теңдеуді интегралдау керек 
A) 
$$$ 173
Біртекті теңдеуді көрсетіңіз:
A) 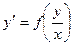
$$$ 174
1-ші ретті сызықтық теңдеуді төмендегі әдіспен шешуге болады
B) 
$$$ 175
 теңдеуінің түрін анықтаңыз
теңдеуінің түрін анықтаңыз
C) Бернулли
$$$ 176
 теңдеуін толық дифференциал теңдеуге тексеріп, шешімін табу керек
теңдеуін толық дифференциал теңдеуге тексеріп, шешімін табу керек
D) 
$$$ 177
Туындысы бойынша айқындалмаған  теңдеуін шешіңіз
теңдеуін шешіңіз
B) 
$$$ 178
 теңдеуін шешу үшін қандай ауыстыру жасаймыз
теңдеуін шешу үшін қандай ауыстыру жасаймыз
C) 
$$$ 179
 теңдеуін шешу керек
теңдеуін шешу керек
A) 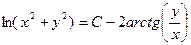
$$$ 180
 теңдеуін
теңдеуін  бастапқы шарттарын қанағаттандыратын шешімін табу керек
бастапқы шарттарын қанағаттандыратын шешімін табу керек
A) 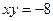
$$$ 181
Біртекті теңдеулерді көрсетіңіз:
A) 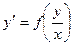
$$$ 182
Айнымалылары бөліктенетін теңдеуді көрсетіңіз:
C) 
$$$ 183
1-ші ретті сызықтық теңдеуді төмендегі әдіспен шешуге болады
B) 
$$$ 184
 теңдеуіне төмендегі ауыстыру енгізіп, сызықтық теңдеуге келтіреміз
теңдеуіне төмендегі ауыстыру енгізіп, сызықтық теңдеуге келтіреміз
E) 
$$$ 185
Егер кез келген берілген қатынас тәуелсіз айнымалы мен оның белгісіз функцияларымен оның туындыларын байланыстырып тұрса, онда оны ........ деп атайды
D) дифференциалдық теңдеу
$$$ 186
Теңдеуді интегралдау керек 
A) 
$$$ 187
 функциясы
функциясы  -ретті біртекті функция деп аталады, егер
-ретті біртекті функция деп аталады, егер  және
және  ,
,  үшін ..... орындалса
үшін ..... орындалса
A) 
$$$ 188
 теңдеуінде
теңдеуінде  болса, теңдеу
болса, теңдеу
A) 3-ретті дифференциалдық теңдеу
$$$ 189
Коши есебі былай қойылады.  теңдеуінің шексіз көп шешімдері ішінен төмендегі шартты қанағаттандыратын
теңдеуінің шексіз көп шешімдері ішінен төмендегі шартты қанағаттандыратын  шешімін табу керек.
шешімін табу керек.
C) 
$$$ 190
Біртекті теңдеуді шешу үшін енгізілетін айнымалы:
E) 
$$$ 191
Теңдеуді интегралдау керек 
A) 
$$$ 192
1-ретті сызықтық дифференциалдық теңдеуді интегралдау үшін Бернулли әдісін анықтаңыз
C) 
$$$ 193
 теңдеуінің жалпы шешімі:
теңдеуінің жалпы шешімі:
D)& 
$$$ 194
 Коши есебін шешіңіз:
Коши есебін шешіңіз:
C) 
$$$ 195
 дифференциалдық теңдеуі үшін
дифференциалдық теңдеуі үшін  болғанда изоклина теңдеуі келесі түрге ие болады:
болғанда изоклина теңдеуі келесі түрге ие болады:
D) 
$$$ 196
 дифференциалдық теңдеуі үшін
дифференциалдық теңдеуі үшін  болғанда изоклина теңдеуі келесі түрге ие болады:
болғанда изоклина теңдеуі келесі түрге ие болады:
C) 
$$$ 197
 дифференциалдық теңдеуі үшін
дифференциалдық теңдеуі үшін  болғанда изоклина теңдеуі келесі түрге ие болады:
болғанда изоклина теңдеуі келесі түрге ие болады:
E) 
$$$ 198
 теңдеуінің типін анықтаңыз:
теңдеуінің типін анықтаңыз:
D) сызықтық теңдеу
$$$ 199
Лагранж теңдеуін көрсетіңіз:
E) 
$$$ 200
Коши есебінің ерекше және дербес шешімін табыңыз: 
E) 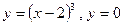 .
.
 2020-01-14
2020-01-14 391
391






