СОДЕРЖАНИЕ
1. Решение по движении материальных точек
2. Решение по уравнению изменения кинетической энергии
3. Решение по движению системы (по принципу Даламбера)
Решение по движении материальных точек
Груз D массой m, получив в точке А начальную скорость  движется в изогнутой трубе АВС, расположенной в вертикальной плоскости: участок АВ – наклонный; участок ВС – горизонтальный.
движется в изогнутой трубе АВС, расположенной в вертикальной плоскости: участок АВ – наклонный; участок ВС – горизонтальный.
На участке АВ на груз кроме силы тяжести действует постоянная сила  (ее направление показано на рисунке) и сила сопротивления среды R, зависящая от скорости V груза (направлена против движения): трение груза о трубу на участке АВ пренебречь.
(ее направление показано на рисунке) и сила сопротивления среды R, зависящая от скорости V груза (направлена против движения): трение груза о трубу на участке АВ пренебречь.
В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действует сила трения (коэффициент трения о трубу f = 0,2) и переменная сила  , проекция которой F1 задана в таблице.
, проекция которой F1 задана в таблице.
Считая груз материальной точкой и зная расстояние АВ = t или время t1 движение груза от точки А до точки В, найти закон движения груза на участке ВС, т.е. x = f(t), где x = BD.

Дано:
m=1,8 кг.
 = 24 м/с
= 24 м/с
Q = 5H
R = 0,3V
t = 2 c
F = 2 
F = 0,2
Составляю дифференциальное уравнение движения точки на участке АВ:

 Н
Н






Интегрируя, получaю:

При t=0; ⟶



При t=2c:




На участке BC:

Составляю дифференциальное уравнение:

Fmp = f N; N=P=18 Н
Fmp = 0,2 * 18=3,6 Н



Интегрируя, получаю:

При t=0; 


Интегрируя, получаю:

При t=0; ⟶ x=0; 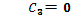
Таким образом уравнение движения примет вид:

Решение по уравнению изменения кинетической энергии
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней  = 0,3 м.,
= 0,3 м.,  = 0,1 м. и радиусом инерции относительно оси вращения
= 0,1 м. и радиусом инерции относительно оси вращения 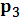 = 0,2 м. блока 4 радиуса
= 0,2 м. блока 4 радиуса  = 0,2 м., и катка (или подвижного блока) 5.
= 0,2 м., и катка (или подвижного блока) 5.
Тело 5 считать сплошным однородным цилиндром, а массу блока 4 – равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3; участки нитей параллельны соответствующим плоскостям. К телу 5 прикреплена пружина с коэффициентом жесткости c.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент M сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным  = 0,2 м.
= 0,2 м.
Все катки, включая и катки обмотанные нитями катятся по плоскостям без скольжения.
В данной задаче не буду изображать груз 2, т.к.  = 0.
= 0.
Дано:
 = 8 кг.
= 8 кг.
 = 0
= 0
 = 5 кг.
= 5 кг.
 = 0
= 0
 = 6 кг.
= 6 кг.
С = 280 Н/м.
М = 0,8Н*м.
𝝎3 -?
Решение: Тело 1 совершает поступательное движение; тела 3,4 – вращательное; тело 5 – плоскопараллельное движение.

Из теоремы об изменении кинетической энергии материальной точки следует:  - =
- = 
 = 0, т. к. в начальном движение система находилась в покое.
= 0, т. к. в начальном движение система находилась в покое.
Так как Т =  +
+ 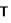 +
+  , то кинетическая энергия для тела 1 (поступательное движение): =
, то кинетическая энергия для тела 1 (поступательное движение): = 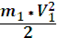 ;
;
Для тела 3 ⟶ 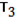 =
=  , момент инерции тела 3 относительно оси проходящей ч/з центр масс будет равен
, момент инерции тела 3 относительно оси проходящей ч/з центр масс будет равен 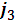 =
=  =0,2;
=0,2;
Для тела 5 ⟶  =
= 
 момент инерции тела 5 будет равен
момент инерции тела 5 будет равен
 =
=  = 0,03
= 0,03
 =
=  =
=  = 3,33
= 3,33 
 =
=  *
*  = 3,33
= 3,33  *0,1 =0,333
*0,1 =0,333 
 =
=  = 0,3
= 0,3  ⟶
⟶  0,3
0,3  = 0,1
= 0,1 
 =
=  =
=  = 0,5
= 0,5 
 =
= 
 =
=  =
=  0,05
0,05 
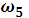 =
=  ;
;  =
=  = 0,1м. ⟶
= 0,1м. ⟶ 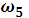 =
=  = 0,5
= 0,5 
 =
=  = 0,36
= 0,36 
 =
=  = 0,1
= 0,1 
 =
= 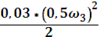 +
+  = 0,003
= 0,003  +0,0075
+0,0075  = 0,01125
= 0,01125 
T =0,36  = 0,47125
= 0,47125 
Далее определяю работу сил:
A(F) = 
 =320*0,2+180*
=320*0,2+180* 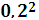 = 64+7,2 = 71,2 Дж.
= 64+7,2 = 71,2 Дж.
 =
=  =
=  = 0,67 рад.
= 0,67 рад.
 = 0,67*0,1 = 0,067 м.
= 0,67*0,1 = 0,067 м.
 =
=  =
=  = 0,335 рад.
= 0,335 рад.
 = 0,067 м.
= 0,067 м.
 =
=  = 0,0335 м.
= 0,0335 м.
A(  )=
)=  *cos 60˚ *
*cos 60˚ *  g* cos 60˚ = 8*10*0,5*0,2 = 8 Дж.
g* cos 60˚ = 8*10*0,5*0,2 = 8 Дж.
A(  ) = -
) = -  *
* 
 = f*
= f* 
 *cos 30˚=8*10*0,87 = 69,6 Н.
*cos 30˚=8*10*0,87 = 69,6 Н.
 69,6 = 6,96 Н
69,6 = 6,96 Н
A(  ) = - 6,96 *
) = - 6,96 * 
A(  = - М*
= - М*  = - 0,8 * 0,67 = - 0,536 Дж.
= - 0,8 * 0,67 = - 0,536 Дж.
A(  )=
)=  *cos 45 ˚ *
*cos 45 ˚ * 
A() = -  = -
= -  = -0,157 Дж.
= -0,157 Дж.
 = 71,2+8-1,392- 0,536 – 1,4271 – 0,157 = 75,6879 Дж.
= 71,2+8-1,392- 0,536 – 1,4271 – 0,157 = 75,6879 Дж.
0,47125  = 75,6879 Дж.
= 75,6879 Дж.
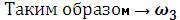 =
= 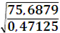 = 12,67
= 12,67
 2020-01-14
2020-01-14 119
119







