Основные теоремы о пределах

Теорема 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов:

Теорема справедлива для алгебраической суммы любого конечного числа функций.

Теорема 2. Функция может иметь только один предел при .

Теорема 3. Предел произведения двух функций равен произведению их пределов:

.

Следствие 1. Постоянный множитель можно выносить за знак предела:

Следствие 2. Предел степени с натуральным показателем равен той же степени предела: .

Теорема 4. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю.

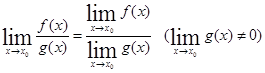
Примеры:

1) = = = =

= = =

2) =

=

3)

Первый замечательный предел

Второй замечательный предел

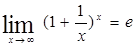 или

Примеры:

Вычислить:

1) .

2) .

3)

4) = = =

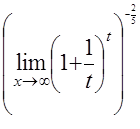№2. Найти пределы:

№3. Найти пределы:

Порядок проведения работы:

1. Используя теоретические сведения выполнить предложенное преподавателем задание

2. Соответствующим образом оформить работу

Лист 1.   Практическая работа по теме «Вычисление пределов»     Выполнил:__________ (ФИО) группа:_____________   Проверил:__________ Оценка:____________

Лист 2.   № примера   Решение:   Ответ:

Оформление работы: