2020-01-14
181
Сравним между собой две употребляемые формы записи передаточной функции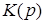 
ПФ второго порядка (см. табл. 1, формы 1, 2),
можно видеть, что
= 
, 
=b1/b2, 
в результате получаем = ; 
= 
= 
; 
= 
.
Таким образом, для определения параметров (параметрического синтеза) семи пассивных элементов (
, 
, 
– 
) заданной цепи, удовлетворяющей заданным электрическим свойствам, имеем три уравнения. Недостающие уравнения получим, наложив следующие дополнительные условия. Исходя из сокращения номенклатуры номиналов элементов и в целях обеспечения относительно большого входного сопротивления каскадов положим = = 
=10нФ, = 
= 
=1000 Ом.
Воспользуемся полученными в пункте 1 выражениями для коэффициентов 
, 
дробно-рационального представления передаточной функции 
через параметры элементов схемы , , – . В результате подстановки получим
Отсюда находим
R5= 
R3=114 ОМ
Параметры всех элементов фильтра определены. Их конкретные значения выбраны в соответствии с рядами номинальных значений сопротивлений резисторов и емкостей конденсаторов.
|
|
|
Численные значения коэффициентов дробно-рационального представления передаточной функции 
= 
рассчитанного ФНЧ равны:
 =1.013∙10-14;
|  =1.277 ∙10-10
|
 =1.299∙10-21;
| |
 =2.099∙10-16;
|
Нули 
и полюсы 
фильтра определим из уравнений
M(p0)= 1.013∙10-14 p0=0
N(p*)=1.299∙10-21p*2 +2.099∙10-16 p* +1.277 ∙10-10 =0
Получаем, что фильтр имеет один нуль и два комплексно-сопряженных полюса: 
=0 рад/с; 
=-80792±ј∙302950рад/с.
Графическое изображение расположения нулей и полюсов функции на плоскости операторной переменной р=α+jwназывается диаграммой или картой нулей и полюсов
Полюсно–нулевая карта, построенная по этим данным, представлена на рис.4.
