2020-01-14
190
Уравнение комплексной передаточной функции 
может быть получено из уравнения операторной передаточной функции 
при замене операторной переменной 
на мнимую частоту 
:
= 
.
В свою очередь, после выделения действительных 
, 
и мнимых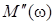 
, 
составляющих числителя 
и знаменателя 
дробного выражения комплексной передаточной функции
= 
= 
,
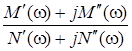легко находятся уравнения АЧХ и ФЧХ цепи:
= 
= 
;
= 
= 
- 
;
= 
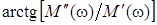при 
;
= 
при 
, 
;
= 
при , 
;
= 
при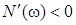 
;
= 
при 
, 
;
= 
при ,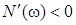 
.
Уравнения АЧХ и ФЧХ фильтра получим из дробно-рационального выражения его операторной функции передачи:
= 
Положив = , получим выражение для комплексной передаточной функции:
= 
= 
=
= 
Определив модуль этого комплексного выражения, найдем уравнение АЧХ фильтра:
= 
= 
= 
Для нахождения уравнения ФЧХ нужно найти аргумент функции 
:
= 
= 
= 
- .
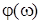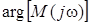Оставаясь действительным, полином числителя
= 
при любой частоте не меняет свой знак. Поэтому 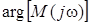=0 при любой 
( ≥0).
У полинома знаменателя
= 
действительная часть
= 
при частоте ω>313538 рад\с меняет знак. В зависимости от знака действительной части аргумент комплексной функции будет определяться по разным формулам:
= 
при 0≤ 
<313538 рад/с ( >0);
= 
при 
≥313538 рад/с ( <0).
= 
при =313538 рад/с
Таким образом, уравнение ФЧХ будет выглядеть следующим образом
=- 
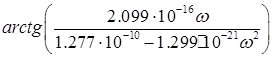
при 0≤ <313538рад/с
= 
при >313538рад/с
= 
при =313538 рад/с
По полученным уравнениям (задавая с определенным шагом значения 
и вычисляя соответствующие значения =2π 
) можно построить графики АЧХ 
и ФЧХ 
фильтра, а также диаграмму АФХ. Для построения амплитудно–фазовой характеристики (АФХ или частотного годографа) целесообразно воспользоваться не показательной формой комплексного параметра KU(jf)=K(ω)ехр(jφ(f)),а алгебраической КU(jf)=A(f)+jB(f)=K(f)cosφ(f) + j K(f)sinφ(f).
По графику определим частоту среза 
полосу пропускания 
, крутизну спада амплитудно-частотной характеристики 
:
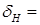Дб/дек 
Дб/дек
н=39300 Гц
н=63300Гц
→63300-39300=24000Гц
Расчет частотных характеристик всегда проводят в определенном диапазоне частот, в котором проявляются основные частотные свойства электрической цепи. Величину диапазона частот можно определить по полюсно-нулевой карте операторной функции.
В качестве нижней граничной частоты fн можно принять значение, близкое к величине
где Smin – расстояние от начала координат до ближайшей особой точки (нуля или полюса)
Это расстояние определяется как модуль особой точки: S =p0или S=p*.
За верхнюю граничную частоту fв можно взять значение
где Smax – расстояние от начала координат до самой удаленной особой точки. Рассчитаем граничные частоты для нашего примера.
p0=0 рад/c, 
Следовательно, Smin=p0, Smax=p*,
 |
