2020-01-14
351
Формулам приписываются значения типа (И, Л) по следующим правилам:
*Формула вида А & В имеет значение И, если и только если значение А есть И и значение В есть И. В противном случае – если значение А, или значение В, или значения обоих вместе есть Л – формула этого вида имеет значение Л.
*Формула вида А 
В имеет значение И если и только если – какая-нибудь из ее составляющих – А или В – имеет это значение.
*Значение А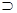 
есть И если и только если имеет место какой-нибудь из случаев (или оба): значение А = Л или значение В = И.
| (p q)
и и и
л и и
и и л
л л л
|
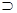л
и
л
и
|  p
л и
и л
л и
и л
|
*Значение формулы вида А есть И если и только если значение А = Л.
При вычислении истинностных значений сложных высказыва-ний вида (p q) 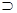p при заданных значениях его составляю-щих: значение р – Л (ложь), q – И (истина). Для вычисления всего выраже-ния надо вычислить значе-ния его составляющих (p q) и p.
Законы логики как тождественно-истинные формулы логики высказываний.
Зак. мышления или лог. заключений- это необходимая существ. связь мыслей в проц. рассуждения.
Закон тождества - всякая мысль в процессе рассуждения должна быть тождественна сама себе, т.е. нельзя отождествлять различные мысли (подмена понятий) и тождеств. мысли принимать за нетождеств.. p→p.
Закон не противоречия - два несовместимых друг с другом суждения не могут быть одновременно истинными, хотя бы одно из них ложно. не(p и не p), не p- любое высказывание, искл. p. Зак. действ. в отнош. всех несовместных сужд..
Закон искл. третьего - два противоречащих сужд. не могут быть одновременно ложными, одно из них необходимо истинно. a есть либо b, либо не b.
Закон достаточного основания - всякая мысль признаётся ист., если она имеет достаточное основание. Аргументация утверждения. a→b.
