Язык логики высказываний (алфавит, понятие формулы). Табличное определение логических связок

Основные синтаксические категории языка логики высказываний, из которых должны строиться высказывания и высказывательные формы, называемые формулами языка логики высказываний, перечень знаков этих категорий называют исходными символами или алфавитом языка.

Алфавит логики высказываний:

1.Пропозициональные переменные p, q, r, s, а также эти же символы с числовыми индексами: p₁, p_2, … p_n, …

2.логические константы (связки): & (конъюнкция),  (дизъюнкция), 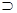 (импликация),  (отрицание);

3.Технические знаки: (– левая скобка,) – правая скобка.

Формула – это осмысленное выражение логики высказываний.

Формулы логики высказываний:

1.Любая пропозициональная переменная (например, p, q, r, s) есть уже формула.

2.Если А и В – формулы, то (А & B), (A  B), (А  В), (A 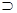 B), (А  В) тоже являются формулами.

3.Если А – формула, то  А – формула.

4.Ничто иное не есть формула.

Табличное определение логических связок.

Знак	Название	Соответст. в рус. языке
	отрицание	«не», «неверно, что»
&	конъюнкция	«и», «а», «но»
	дизъюнкция	«или»
	строгая дизъюнкция	«или…или», «либо…либо»
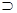
	импликация	«если…, то…», «когда…, то…»
	эквиваленция	«если и только если», «тогда и только тогда»