Розділ 2. Теорема Піфагора у просторі або стереометричний аналог теореми Піфагора

 

Метод аналогії є одним з ефективних і розповсюджених методів математики. Його застосування приводить до плідних і часто до неочікуваних результатів.

Деякі властивості трикутника і тетраедра схожі, а деякі геометричні поняття, пов’язані з трикутником, мають просторові аналоги: наприклад, сторона трикутника – грань тетраедра, довжина сторони – площа грані, вписане коло – вписана сфера, площа – об’єм,бісектриса кута – бісектор двогранного кута тощо. Багато теорем про трикутники, якщо замінити в їх формулюванні планіметричні терміни відповідними стереометричними і конкретно сформулювати, то вони перетворюються в теореми про тетраедри. Однією з таких є аналог теореми Піфагора в стереометрії.

Означення. Якщо три ребра, які виходять з однієї вершини тетраедра, попарно ортогональні, то тригранний кут, що визначається ними, називається прямим, а тетраедр – прямокутним.

Теорема (стереометричний аналог теореми Піфагора).У прямокутному тетраедрі квадрат площі грані, що лежить проти прямого тригранного кута, дорівнює сумі квадратів площ решти граней.

Доведення 1. Нехай у прямокутному тетраедрі OABC

 

 (Рис.2.1)

 

Доведемо, що

 

 

Маємо:

 

 (1)

 

У Δ АВС:

 

,  (2)

 

Площу трикутника АВС обчислимо за формою Герона

 

, де

 

Виконаємо перетворення:

 

,

 

.

 

Використовуючи (2), (3), одержимо:

 

тобто (4)

 

Враховуючи (1), (4), одержимо

 

 

 

Розглянемо доведення, в якому використовується метод проекцій

Доведення 2

Нехай у прямокутному тетраедрі ОАВС грані ОВС, ОАС, ОАВ утворюють з основою АВС кути  відповідно. Оскільки точка О проектується в ортоцентр Н трикутника АВС, то лінійні кути двогранних кутів при основі утворюватимуться висотами відповідних граней: 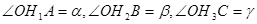(Рис. 2.2).Спроектуємо висоту ОН на ребра прямого тригранного кута, одержимо: ОА₁=ОН (Рис. 2.3), аналогічно ОВ₁=ОН , OC₁=OH .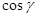

У прямокутному паралелепіпеді з діагоналлю ОН і ребрами ОА₁, ОВ₁, ОС₁ справджується рівність

 

 

або ,

звідки  (1)

 

Оскільки 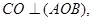то ΔAOB – ортогональна проекція ΔАВС, аналогічно ΔAOC – ортогональна проекція ΔАВС і ΔBOС – ортогональна проекція ΔАВС.

Маємо:

 

,

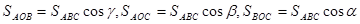звідси . (2)

 

Враховуючи (1) і (2), одержимо:

 

, або .

 

Пропонуємо інші доведення теореми Піфагора для прямокутного тетраедра.

Доведення 3

Нехай у прямокутному тетраедрі ОАВС

 

, (Рис. 2.4).

 

Побудуємо висоту СН трикутника АВС і сполучимо точки О і Н.

Маємо: СН – похила, ОН – її проекція, СН АВ. За теоремою про три перпендикуляри ОН АВ. Знайдемо площу трикутника АВС:

 

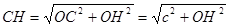З ΔСОН ( О = 90°)  (2)

 

Знайдемо ОН, для цього виразимо площу трикутника АОВ через катети, тобто

 

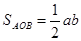(3),

теорема піфагор площина простір

і через гіпотенузу АВ та висоту ОН, опущену на неї, тобто

 

або (4)

 

З рівностей (3), (4)

 

,

звідки 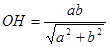. (5)

 

Враховуючи (2), (5), одержимо:

 

(6)

Спосіб 1. Враховуючи (1), (6) одержимо:

 

 

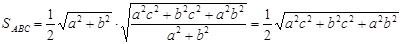
Тоді

 

.

Спосіб 2. Можна використати формулу проекцій

 

 

Оскільки

 

 і

,

то ,

звідки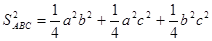

або .

Доведення 4. Нехай у тетраедрі ОАВС 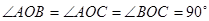, , лінійний кут двогранного кута при ребрі АВ 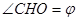 (Рис. 2.5). Припустимо, що виконується рівність

 

. (1)

 

Оскільки ΔАОВ – ортогональна проекція ΔАВС, то

 

 (2)

 

Враховуючи рівності (1) і (2), одержимо:

 

. (3)

З ΔАОВ ( О = 90°) ,

тоді ,

звідки , або 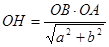. З ΔСОН ()

 

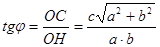
Крім цього,

 

 

Формула (3) набуває вигляду

 

,

тобто

 

Останній вираз є вірною рівністю, одержаною з рівності (1) за допомогою тотожних перетворень, тому можна зробити висновок: початкове припущення вірне і справедлива теорема: У прямокутному тетраедрі квадрат площі грані, що лежить проти прямого тригранного кута дорівнює сумі квадратів площ решти граней.

 

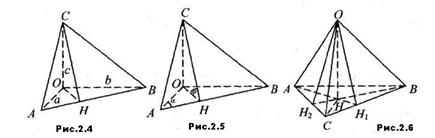
Доведення 5. Нехай ОН – висота прямокутного тетраедра ОАВС з прямим тригранним кутом при вершині О, тоді АН₁ – висота ΔАВС (Рис.2.6).

 

З ΔАОН₁  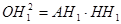(наслідок з теореми Піфагора)

 

Помноживши цю рівність на , одержимо:

 

 

або ,

або  (1)

 

Аналогічно одержимо:

 

, (2)

 (3)

 

Додамо почленно рівності (1), (2), (3), одержимо

 

.

 

Таким чином,

 

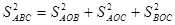
Доведення 6. Нехай у тетраедрі ОАВС , ΔАНС – ортогональна проекція ΔАОС на площину трикутника АВС (Рис.2.6).

Позначимо  - лінійний кут двогранного кута при ребрі АС. Тоді

 

 (1)

 

Оскільки ΔАОС – ортогональна проекція ΔАВС, то

 

 (2)

 

З (1), (2) слідує

 

,

звідки . (3)

 

Аналогічно одержимо

 

 (4),

.

 

Додамо почленно (3), (4), (5), одержимо:

 

.

 

Таким чином,

 

.

Доведення 7. Нехай у прямокутному тетраедрі ОАВС , .Виберемо прямокутну декартові систему координат  так, що вісь сумістилась з прямою ОА, вісь  - з прямою ОВ, а вісь  - з прямою ОС і розглянемо вектори  і  (Рис. 2.7). Маємо в :

Оскільки

 

^ , .

 

Отже,

 

 (1)

Обчислимо

 

 (2),

 (3)

 

Враховуючи (1), (2), (3), одержимо

 

,

звідки .

З ΔАСН .

Маємо .

 

Тоді

 

 

Оскільки

 

,

то ,

звідси  або

Доведення 8. Для обчислення площі трикутника АВС (Рис.2.7) використаємо геометричне тлумачення векторного добутку двох векторів, а саме:

 

 

Оскільки

 

,

 

то одержимо:

 

Тоді

Таким чином,

 

,

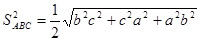звідки

 

Враховуючи, що

 

,

 

остаточно одержимо

 

Доведення 9. У вибраній системі координат  координати вершин тетраедра ОАВС (Рис.2.8) набудуть вигляду: .

Об’єм тетраедра можна обчислити за формулою:

 

,

 

де  () – координати вершин тетраедра.

Застосуємо цю формулу

 

. (1)

З іншого боку

 

 (2),

 

де ОН – висота тетраедра (Рис. 2.6).

Висоту ОН знайдемо як відстань від точки О до площини трикутника АВС. Для цього складемо рівняння площини (АВС) "у відрізках на осях":

 

 

або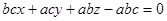

 

Тоді

 

. (3)

З (1), (2), (3) слідує

 

,

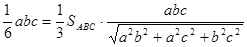звідки

або .

 

Доведення 10. Використаємо (рис.2.8) і позначення на ньому. Висоту ОО₁ обчислимо як відстань між точками О і О₁, для цього складемо рівняння прямої ОО₁. Рівняння площини (АВС) має вигляд

 

 

(див. розв’язання 9),

де — вектор нормалі.

Оскільки , то 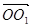(як два перпендикуляри до площини).

Таким чином, вектор — напрямний вектор прямої ОО₁. Канонічні рівняння прямої ОО₁ набудуть вигляду:

 

,

 

звідси одержимо параметричні рівняння ОО₁:

 

 

Обчислимо координати точки О₁, розв'язавши систему рівнянь:

 

Тоді  (1)

 

Обчислимо об’єм тетраедра ОАВС за формулою

 

, тоді . (2)

 

Враховуючи, що

 

,

 

одержимо:

 

,

звідки  

або .

Доведення 11. Теорему Піфагора для прямокутного тетраедра можна розглядати як наслідок теореми косинусів для довільного тетраедра [3], яка формулюється так: квадрат площі будь-якої грані тетраедра дорівнює сумі квадратів площ інших граней без подвоєних добутків площ цих граней, взятих попарно, на косинус двогранних кутів між ними, тобто

 

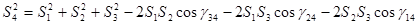. (1)

 

У прямокутному тетраедрі двогранні кути 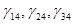прямі і з теореми косинусів (1) одержимо співвідношення

 

 

 

площі граней - катетів, а - площа грані - гіпотенузи.

Таким чином, стереометричний аналог теореми Піфагора можна сформулювати так: У прямокутному тетраедрі квадрат площі грані гіпотенузи дорівнює сумі квадратів площ граней - катетів.

Зауваження. Має місце наслідок з цієї теореми: площі граней - катетів є середніми геометричними між площею грані — гіпотенузи і площами їх проекцій на грань - гіпотенузу (див. доведення 5).

 

 

Висновок

 

Мабуть, найпопулярнішою з усіх теорем є теорема Піфагора. Причинами такої популярності є простота, краса, значення. Справді, теорема Піфагора проста, але не очевидна. Це поєднання двох суперечностей і надає їй особливої привабливості.Теорема Піфагора - важливий інструмент геометричних обчислень. Використовуючи її, можна обчислити у планіметрії діагональ квадрата і прямокутника, висоту, медіану, бісектрису рівностороннього або рівнобедреного трикутника, висоту рівностороннього трикутника, радіуси вписаного і описаного кіл правильного трикутника, рівнобедреного трикутника тощо.

Теорема Піфагора використовується при розв’язанні трикутників, у теорії площ.

У стереометрії теорема Піфагора застосовується при обчисленні висоти, ребра або апофеми правильної піраміди, при вивченні многогранників, тіл обертання та їх комбінацій.

Взагалі, перелічити з достатньою повнотою всі випадки, де використовується теорема Піфагора в геометрії неможливо. Вона має не лише теоретичний характер, а й широко використовується на практиці при розрахунках покрівель дахів, верхніх частин вікон у будинках готичного і романського стилю, паркетуванні підлоги тощо.

З теореми Піфагора випливає чимало наслідків, які є її вінцем, зокрема:

- у прямокутному трикутнику будь – який катет менший від гіпотенузи;

- косинус кута а менше одиниці для будь – якого гострого кута а;

- якщо до прямої з однієї точки провести перпендикуляр і похилі,то похилі більші перпендикуляра; рівні похилі мають рівні проекції; з двох похилих більша та, у якої проекція більша.

Сама теорема Піфагора є наслідком теореми: косинус кута залежить лише від градусної міри кута. Тому, якщо теорему Піфагора «вплести» у вінок її наслідків, то отримаємо вінок наслідків теореми про косинус кута.

Із означень sinα, cosα, tgα випливають такі властивості:

- катет, протилежний куту α, дорівнює добутку гіпотенузи на sinα;

- катет, прилеглий до кута α, дорівнює добутку гіпотенузи на cosα;

- катет, протилежний куту α, дорівнює добутку другого катета на tgα;

- катет прямокутного трикутника є середнє пропорційне між гіпотенузою і його проекцією на гіпотенузу;

- висота прямокутного трикутника, опущена з вершини прямого кута, є середнє пропорційне між проекціями катетів на гіпотенузу.

Вся геометрія складеться з таких прекрасних віночків, слід лише придивитись до них, звертати на них увагу, порівнювати, запам’ятовувати і вміло використовувати їх при розв’язанні задач.

 

Література

 

1. Боровик В.Н., Зайченко І.В., Кобко Л.М. «Гармонія і естетика трикутника». Навчальний посібник для студентів вищих навчальних закладів – 2-е вид., виправл. і доп.. Рекомендовано МОН України – К.: Освіта України, 2007. – 180с.

2. Кобко Л.М. «Аналогія: планіметрія–стереометрія в таблицях». Навчальний посібник для студентів педагогічних вищих навчальних закладів. – Чернігів, 2008.- 64с.

3. Кобко Л.М. «У світі геометрії». Навчально–методичний посібник для студентів педагогічних вищих навчальних закладів. – Чернігів, 2009.- 209с.