2020-01-14
89
Доведення 1. На гіпотенузі і катетах побудуємо квадрати і виконаємо додаткові побудови, які видно на рисунку 1. Тоді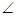 
NAB = 90° + 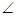САВ,
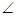САЕ =90° + 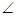САВ. Отже, 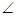NАВ = 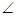САЕ. Крім цього, NА = СА, АВ = АЕ.
Таким чином, за першою ознакою рівності трикутників маємо: ΔNAB = ΔCAE. Але SΔNAB = 
NA·NK = SΔANRC, SΔCAE = AE·EH = SAEHR. Порівнюючи останні три рівності, дістанемо: SANKC = SAEHR. (1) Аналогічно, 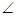ABE = 90° + 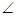ABC, 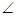CBD = 90° + 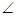ABC. Звідси 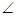ABF = 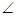CBD. Крім того, AB – DB, CB – FB. Тоді за першою ознакою рівності трикутників ΔABF = ΔDBC. Але SΔABF = 
BF·QF = SBCQF, SΔDBC = 
BD·HD = SHRBD. З цих рівностей одержимо: SBCQA = SHRBD. (2) Додамо почленно рівності (1) і (2):
SANKC + SBCQF = SAEHR + SHRBD, але SAEHR + SHRBD = SAEDB.
Таким чином, SANKC + SAEDB або b2 + a2 = c2
Рис. 1
Рис. 2
Доведення 2
Побудуємо ΔBDE = ΔACB так, щоб B 
CD (рис 2).
Тоді чотирикутник ACDE – трапеція, бо AC || DE як два перпендикуляри до CD. Маємо:
SACDE = 
·CD = 
· 
2 (1)
Крім того, SACDE = SΔABE + 2SΔABC. Трикутник ABE рівнобедрений і прямокутний. Дійсно, якщо позначимо 
АВС = BED = 
, тоді в прямокутному трикутнику BDE DBE = 90° - . За побудовою CBD = 90°.Таким чином, 
ABE = 180° - 
°, SΔABC= 
, SΔABC= 
.
Тоді SACDE= 
(2)
Порівнюючи рівності (1) і (2), дістанемо:
Доведення 3. Побудуємо CD 
AB (рис.3).
Нехай CAB = BCD = 
. Тоді SΔABC = 
sin . Оскільки 
,
SΔABC = 
(1)
Аналогічно: SΔACD = 
(2)
SΔBCD = 
(3)
За побудовою SΔABC = SΔACD + SΔBCD. (4)
З рівностей (1), (2), (3), (4) випливає:
тобто 
Рис.3 
Рис.4
Доведення 4. Впишемо в трикутник АВС коло (О, r) (Рис.4). Тоді:
SΔABC = SΔOAC + SΔOAB = 
Чотирикутник OKCL – квадрат з стороною r. За властивістю дотичних, проведених з точок А та В до кола, маємо: AH = AK = 
, BH = BL = 
.
Тоді
AB = AH + HB = 
З іншого боку
SΔABC = 
.
Таким чином,
Доведення 5
Виконуємо побудови, які показано на рисунку 5 а), 5 б).
Рис.5,а
Рис.5,б
CDMN, TQRE – квадрати зі стороною 
. Тоді SCDMN = STQRE.
За побудовою маємо:
SCDMN = SABLK + 4SΔABC,
STQRE = SPQBC + SACFE + 4SΔABC.
Порівнюючи ці рівності, дістанемо:
SABLK + 4SΔABC = SPQBC + SACFE + 4SΔABC, або
SABLK = SPQBC + SACFE, тобто 
Доведення 6
Побудуємо квадрат CDMN з стороною a+b (Рис.6)
Рис. 6
Тоді ΔАСВ = ΔBDK = ΔKLM = ΔLNA (за двома катетами), звідки
AB = BK = KL = LA = c.
Отже, чотирикутник ABKL – ромб.
Оскільки 
АВК = 90°, то ABKL – квадрат. Маємо:
Порівнюючи останні рівності, дістанемо:
Доведення 7
На сторонах прямокутного трикутника АВС побудуємо квадрати АВКМ, АDЕС, ВСFR. (Pис. 7). Трикутники ЕСF, КLМ і АСВ рівні між собою. АDRВ = EDRF як симетричні відносно прямої DR фігури; ACLM = КLСВ як центрально-симетричні фігури відносно центра квадрата АВКМ; АDRB=АСLМ як відповідні фігури при повороті навколо центра А на кут 90°.
Враховуючи одержані три рівності, маємо:
ADEFRB = ACBKLM, але
SADEFRB = SADEC + 2SΔABC + SBCFR, SACBKLM = SABKM + 2SΔABC.
Отже, SADEC + SBCFR = SABKM, тобто 
Рис.7
Рис.8
Доведення 8
Прямокутний трикутник АСВ з прямим кутом С повернемо навколо точки С на 90° так, щоб він зайняв положення А´СВ´ (Рис. 8).Продовжимо гіпотенузу А´В´ до перетину з АВ у точці D. Відрізок В´D буде висотою трикутника В´АВ.
Розглянемо тепер чотирикутник А´АВ´В. Його можна розкласти на два рівнобедрені трикутники СА´А і СВ´В. Маємо:
ЫΔСФ´Ф = 
б ЫΔСИ´И= 
ю
Таким чином
ЫФ´ФИ´И= ЫΔСФ´Ф + ЫΔСИ´И= 
ю
Трикутники АА´В´ і ВА´В´ мають спільну основу В´А´ і висоти AD і BD відповідно. Тому
ЫФ´ФИ´И= ЫΔАФ´В´ + ЫΔВА´И= 
ю
Порівнявши два вирази для площі чотирикутника А´АВ´В, одержимо:
, тобто 
