2020-01-14
626
Решая уравнение Гельмгольца в цилиндрических системах координат, получаем:
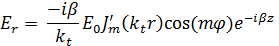
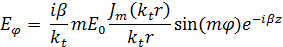
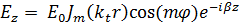
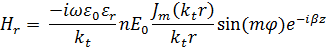
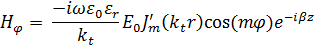
Зная, как изменяются составляющие поля, построим распределение силовых линий в волноводе и представим на рисунке 1.
Рисунок 1 – Распределение силовых линий в круговом волноводе
ИССЛЕДОВАНИЕ СПЕКТРА МОД.
Зная размер волновода и рабочий диапазон частот, определим, какие моды электрического поля могут распространяться в данном волноводе по формуле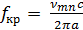 
, где fкр принадлежит рабочему диапазону частот.
Для E мод
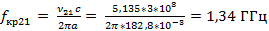
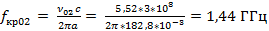
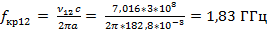
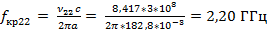
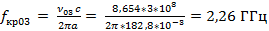
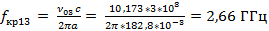
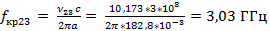
Для H мод
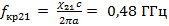
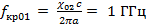
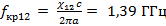
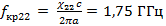
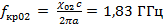
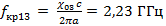
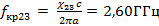
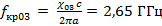
Таким образом, в волноводе с заданными геометрическими параметрами и рабочим диапазоном частот могут распространяться моды: E11, E21, E02, E12, E22, E03, E13, E23 и H01, H12, H22, H02, H13, H23, H03
Волновое число рассчитывается по формуле
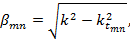где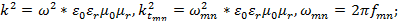 
Откуда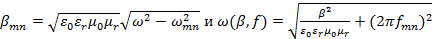 
Для воздуха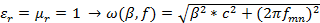 
Построим дисперсионные кривые выше представленных мод в координатах Бриллюэна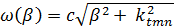 
и представим их на рисунке 2 и 3.
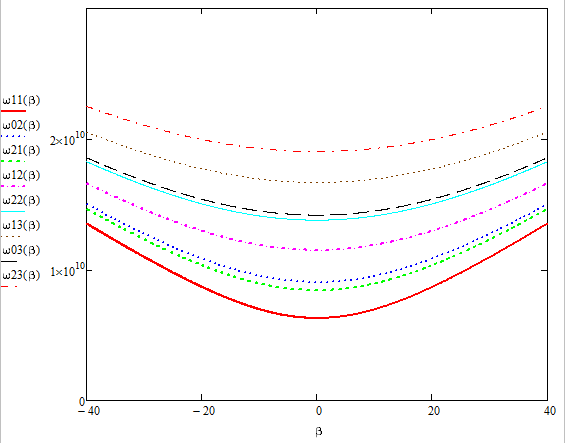
Рисунок 2 – Дисперсионные кривые для разных мод Еmn
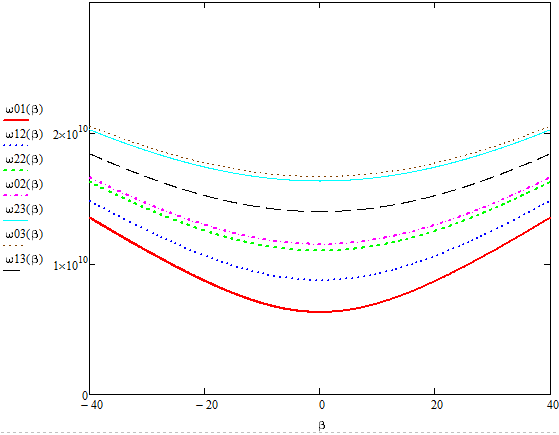
Рисунок 3 – Дисперсионные кривые для разных мод Hmn
ИССЛЕДОВАНИЕ ВЛИЯНИЯ МАТЕРИАЛА ДИЭЛЕКТРИЧЕСКОГО ЗАПОЛНЕНИЯ ВОЛНОВОДА.
Заданный диэлектрик – алюминат лантана LaAlO3 имеет относительную диэлектрическую проницаемость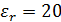 
Построим частотную зависимость волнового сопротивления при воздушном заполнении и заполнении заданным диэлектриком:
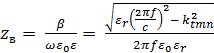(4.1),
где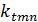 
– поперечное волновое число, f – частота, 
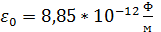– электрическая постоянная, 
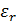– относительная диэлектрическая проницаемость среды.
По 4.1 построим частотные зависимости и представим их на рисунке 4.
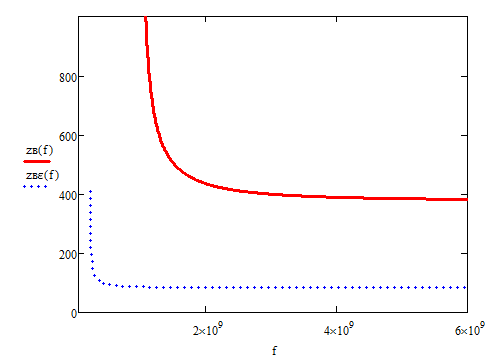
Рисунок 4 – Частотная зависимость волнового сопротивления при разном заполнении волновода (сплошная линия – зависимость при воздушном заполнении, штриховая – заполнение диэлектриком LaAlO3).
По зависимости на рисунке 4 можно сказать, что при заполнении волновода диэлектриком сопротивление в рабочем диапазоне практически не зависит от частоты, в отличие от воздушного заполнения, а значение волнового сопротивление меньше в четыре с половиной раза.
