Заметив это, возьмем сходящийся положительный ряд

h₁+h₂+h₃+...        (h_i>0)

и стремящуюся к нулю последовательность положительных чисел

s₁>s₂>s₃>…,   lim s_i=0.

В силу (1), можно каждому натуральному i соотнести такое натуральное n_i, что mR_ni(s_i)< h_i.

Сделав это, найдем такое i₀, что 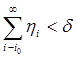(где d число, фигурирующее в формулировке теоремы), и положим .

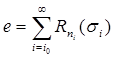Очевидно,

me<d.

Пусть Е_d = Е – е. Установим, что множество Е_d требуемое. Неравенство mE_d > mE - d ясно, так что остается убедиться в равномерности стремления

f_n(x)®f(x)

на множестве Е_d.

Пусть e > 0. Найдем i такое, что i ³ i₀, s_i < e, и покажем, что при k ³ n_i и при всех x Î Е_d будет

|f_k(x) – f(x)| < e,

откуда и будет следовать теорема.

Если x Î Е_d, то х 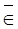e. Значит в частности, x 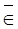R_ni(s_i).

Иначе говоря, при k ³ n_i

x ÎE(|f_k – f|³ s_i),

так что

|f_k(x) – f(x)| <s_i       (k ³ n_i)

и тем более

|f_k(x) – f(x)| < e       (k ³ n_i).

Теорема доказана, ибо n_i зависит только от e, но не от x.

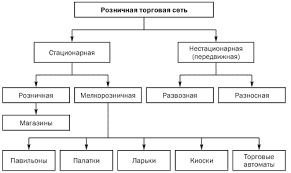
Структура измеримых функций

При изучении какой-нибудь функции сам собою встает вопрос о точном или приближенном представлении ее с помощью функций более простой природы.

Таковы, например, алгебраические вопросы о разложении многочлена на множители или рациональные дроби на простейшие. Таков же вопрос о разложении непрерывной функции в степенной или тригонометрический ряд и т.п.

В этой части мы устанавливаем различные теоремы о приближении измеримых функций функциями непрерывными, т.е. решаем сходный вопрос для измеримых функций. Эти теоремы позволяют нам найти основное структурное свойство измеримой функции выражаемой теоремой 4.

Теорема 1. Пусть на множестве Е задана измеримая, почти везде конечная функция f(x). Каково бы ни было e > 0, существует измеримая ограниченная функция g(x), такая, что mE(f¹g)< e.