В самом деле, взяв две стремящиеся к нулю последовательности

s₁>s₂>s₃>…,          s_n®0,

e₁>e₂>e₃>…,            e_n®0,

построим для каждого n такую непрерывную функцию y_n(x), что

mE(|f-y_n|³s_n)< e_n

Легко видеть, что y_n(x) Þ f(x).

Действительно, какое бы s > 0 ни взять, для n ³ n₀ будет s_n<s, а для таких n

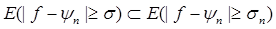
откуда и следует наше утверждение.

Применив к последовательности {y_n(x)} теорему Ф. Рисса мы приходим к последовательности непрерывных функций {y_nk(x)}, которая сходится к функции f(x) почти везде.

Иначе говоря установлена

Теорема 3 (М.Фреше). Для всякой измеримой и почти везде конечной функции f(x), заданной на сегменте [a, b], существует последовательность непрерывных функций, сходящаяся к f(x) почти везде.

С помощью этой теоремы легко устанавливается весьма замечательная и важная

Теорема 4 (Н. Н. Лузин). Пусть f(x) измеримая и почти везде конечная функция, заданная на [a, b]. Каково бы ни было d > 0, существует такая непрерывна функция j(x), что

mE(f ¹ j) < d

Если, в частности, |f(x)| £ K, то и |j(x)| £ K.