Расчетная часть.
Исходные данные:
1. Частота вращения вала - 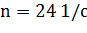 ;
;
Измененная частота вращения вала -  =30 1/ с;
=30 1/ с;
2. Размеры рабочего колеса:
диаметр входа жидкости в рабочее колесо -  ;
;
диаметр выхода жидкости из рабочего колеса - 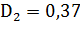 м;
м;
ширина канала на входе жидкости в рабочее колесо - 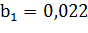 м;
м;
ширина канала на выходе жидкости из рабочего колеса - 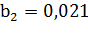 м;
м;
число лопаток на выходе - 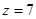 ;
;
толщина лопатки на выходе (по срезу) - 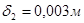 ;
;
конструктивные углы лопатки:
на входе - 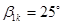 ;
;
на выходе -  .
.
3. Принимаем:
угол входа жидкости в колесо - 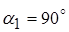 .
.
4. Коэффициенты полезного действия при оптимальном режиме:
объемный К.П.Д. - 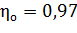 ;
;
гидравлический К.П.Д. - 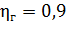 ;
;
дисковый К.П.Д. -  ;
;
механический К.П.Д. - 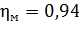 .
.
5. Параметры перекачиваемой жидкости:
коэффициент кинематической вязкости -  см2/сек;
см2/сек;
плотность - 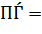 кг/м3.
кг/м3.
Ход расчета.
Расчет характеристик насоса при  .
.
Расчет ведем для оптимального режима, полагая, что при этом режиме углы потока совпадают с конструктивными углами рабочего колеса.
1. Строим треугольник скоростей на входе в рабочее колесо по угла 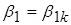 и окружной скорости
и окружной скорости 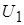 :
:
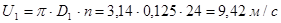
Принимаем масштаб.
По рисунку определяем относительную и окружную скорости:
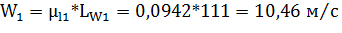 ,
,
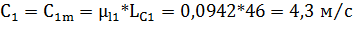 .
.
2. Расход жидкости внутри колеса:
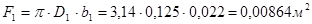 .
.
3. Производительность насоса при оптимальном режиме:
4. Строим план скоростей на выходе жидкости из рабочего колеса по 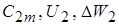 и углу
и углу 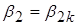 .
.
Окружная скорость:
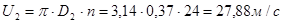
Меридиональная скорость на выходе из колеса:

где 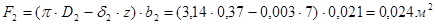 .
.
Окружную составляющую относительного межлопаточного вихря определяется по формуле А. Стодола:
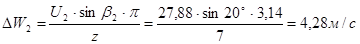 .
.
Задаемся масштабом:;
Определяем длины скоростей:
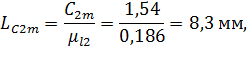
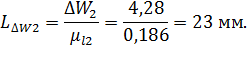
По рисунку определяем:
5. Вычисляем удельную работу лопаток:
Полезная удельная работа насоса.
Полезный напор насоса:
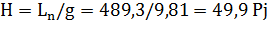 .
.
где 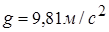 .
.
6. Вычисляем коэффициент быстроходности насоса для оптимального режима:

7. Расчет уточненных значений производительности и удельной энергии. По 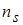 находим вероятные значения К.П.Д. для оптимального режима:
находим вероятные значения К.П.Д. для оптимального режима: 
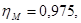
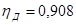 ,
,  .
.
Вычислим уточненные значение насоса при оптимальном режиме:
Полезная удельная работа насоса. Полезный напор насоса:
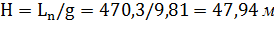 ;
;
Расход жидкости:
8. Мощность на валу насоса:
 ,
,
где 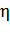 - общий КПД насоса (уточненный)
- общий КПД насоса (уточненный)

Построение комплексной характеристики насоса при работе на воде.
Зная 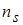 находим в относительных координатах кривые
находим в относительных координатах кривые  ,
, 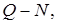
 соответствующие данному насосу. Необходимо построить эти кривые в размерных координатах. Значения в относительных и размерных координатах заносим в таблицу 2.
соответствующие данному насосу. Необходимо построить эти кривые в размерных координатах. Значения в относительных и размерных координатах заносим в таблицу 2.
Таблица 2
| Относительные координаты | 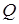
| 0 | 0,2 | 0,4 | 0,6 | 0,8 | 1 | 1,2 |

| 1 | 1,08 | 1,1 | 1,09 | 1,05 | 1 | 0,9 | |
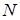
| 0,35 | 0,47 | 0,6 | 0,75 | 0,88 | 1 | 1,15 | |

| 0 | 0,41 | 0,7 | 0,86 | 0,97 | 1 | 0,99 | |
| Размерные Координаты |  м3/с
м3/с
| 0 | 0,007 | 0,014 | 0,021 | 0,028 | 0,035 | 0,042 |
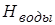 м
м
| 47,94 | 51,78 | 52,73 | 52,25 | 50,34 | 47,94 | 43,15 | |
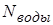 кВт
кВт
| ||||||||
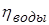
| 0 | 0,3 | 0,5 | 0,63 | 0,71 | 0,732 | 0,725 |
Используя полученные значения, строим комплексную характеристику при работе насоса на воде при  .
.
Пересчет характеристик насоса при п= 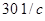 .
.
Расчет ведем для оптимального режима, полагая, что при этом режиме углы потока совпадают с конструктивными углами рабочего колеса.
1. Строим треугольник скоростей на входе в рабочее колесо по угла 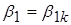 и окружной скорости
и окружной скорости 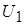 :
:
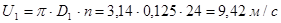
Принимаем масштаб. По рисунку определяем относительную и окружную скорости:
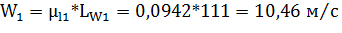 ,
,
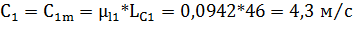 .
.
2. Расход жидкости внутри колеса:
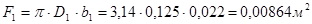 .
.
3. Производительность насоса при оптимальном режиме:
4. Строим план скоростей на выходе жидкости из рабочего колеса по 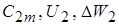 и углу
и углу 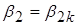 .
.
Окружная скорость:
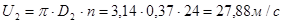
Меридиональная скорость на выходе из колеса:

где  .
.
Окружную составляющую относительного межлопаточного вихря определяется по формуле А. Стодола:
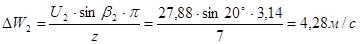 .
.
Задаемся масштабом:;
Определяем длины скоростей:
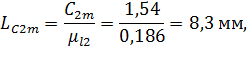
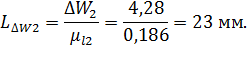
По рисунку определяем:
5. Вычисляем удельную работу лопаток:
Полезный напор насоса:
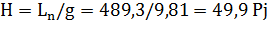 .
.
где 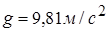 .
.
6. Вычисляем коэффициент быстроходности насоса для оптимального режима:

7. Расчет уточненных значений производительности и удельной энергии.
8. По 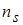 находим вероятные значения К.П.Д. для оптимального режима:
находим вероятные значения К.П.Д. для оптимального режима: 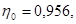
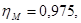
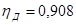 ,
, 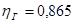 .
.
Вычислим уточненные значение насоса при оптимальном режиме:
Полезная удельная работа насоса. Полезный напор насоса:
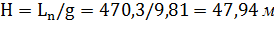 ;
;
Расход жидкости:
9. Мощность на валу насоса:
 ,
,
где 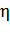 - общий КПД насоса (уточненный)
- общий КПД насоса (уточненный)

10. Построение комплексной характеристики насоса при работе на воде.
Зная 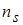 находим в относительных координатах кривые
находим в относительных координатах кривые 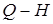 ,
, 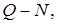
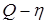 соответствующие данному насосу. Необходимо построить эти кривые в размерных координатах. Значения в относительных и размерных координатах заносим в таблицу 3.
соответствующие данному насосу. Необходимо построить эти кривые в размерных координатах. Значения в относительных и размерных координатах заносим в таблицу 3.
Таблица 3
| Относительные координаты | 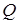
| 0 | 0,2 | 0,4 | 0,6 | 0,8 | 1 | 1,2 |
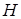
| 1 | 1,08 | 1,1 | 1,09 | 1,05 | 1 | 0,92 | |
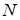
| 0,35 | 0,5 | 0,6 | 0,72 | 0,86 | 1 | 1,13 | |
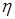
| 0 | 0,42 | 0,7 | 0,87 | 0,96 | 1 | 0,98 | |
| Размерные координаты | 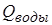
| 0 | 0,014 | 0,028 | 0,042 | 0,056 | 0,07 | 0,084 |
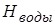
| 120,9 | 130,6 | 132,9 | 131,7 | 126,9 | 120,9 | 111,2 | |
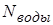
| 34,6 | 49,5 | 59,4 | 71,28 | 85,1 | 99 | 111,8 | |
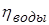
| 0 | 0,35 | 0,58 | 0,72 | 0,8 | 0,84 | 0,82 |
Используя полученные значения, строим комплексную характеристику при работе насоса на воде при 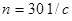 .
.
Проанализировав расчетную часть и графики на рис.13,14,15 можно сделать вывод, что характеристики центробежного насоса (К.П.Д., подача, напор и мощность на валу) при увеличении частоты вращения вала возрастают.
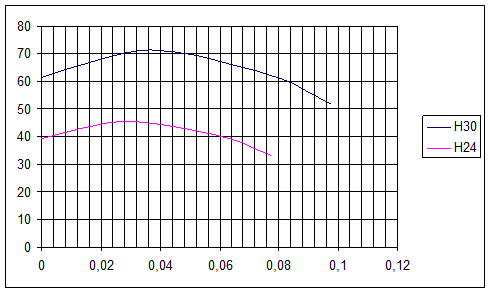
Рис.13. График Q-H
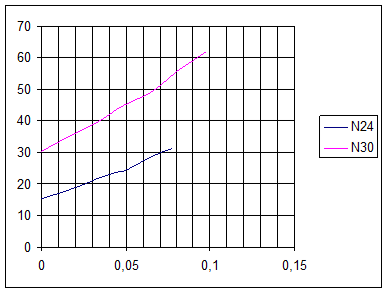
Рис.14. График Q-N
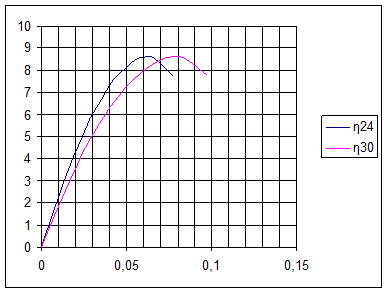
Рис.15. Q-η
 2020-01-14
2020-01-14 217
217








