Числовые значения параметров задачи
| № варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| а, м | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 0,9 | 0,8 | 0,7 |
| I, А | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | 4,5 | 5,0 | 5,5 | :6,0 | 5,0 | 4,5 | 4,0 | 3,5 |
| R, Ом | 2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 10 | 9 | 8 | 7 |
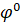
| 30 | 45 | 60 | 90 | 0 | 30 | 45 | 60 | 90 | 0 | 30 | 45 | 60 |
| В 2, Тл | 0,5 | 0,4 | 0,3 | 0,2 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,5 |
| № варианта | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| а, м | 0,5 | 0,4 | 0,3 | 0,2 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0.8 | 0,9 |
| I, А | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | 4.5 | 5,0 | 4,5 | 4,0 | 3,5 | 3,0 |
| R, Ом | 3 | 4 | 5 | 6 | 5 | 4 | 3 | 2 | 3 | 4 | 5 | 6 | 5 |
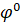
| 90 | 60 | 45 | 30 | 0 | 30 | 45 | 60 | 90 | 0 | 30 | 45 | 60 |
| В 2, Тл | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 0,9 | 0,8 | 0,7 |
3. В соленоиде длиной l, диаметром D исчислом витков N течёт ток силой I. Определить:
1). напряжённость Н 1 и индукцию магнитного поля В 1 внутри соленоида; индуктивность L 1соленоида;
2). потокосцепление  ; магнитный момент Pm этого соленоида; энергию W 1 и объёмную плотность энергии
; магнитный момент Pm этого соленоида; энергию W 1 и объёмную плотность энергии  магнитного поля внутри соленоида; магнитодвижущую силу Fm;
магнитного поля внутри соленоида; магнитодвижущую силу Fm;
3). ошибку  , которую допускаем при нахождении напряжённости Н 1 магнитного поля в центре соленоида, принимая соленоид за бесконечно длинный;
, которую допускаем при нахождении напряжённости Н 1 магнитного поля в центре соленоида, принимая соленоид за бесконечно длинный;
4). индукцию магнитного поля В 2, индуктивность L 2, потокосцепление 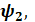 энергию W 2 и объёмную плотность энергии
энергию W 2 и объёмную плотность энергии  магнитного поля внутри соленоида, когда в него вставлен железный сердечник, магнитную проницаемость
магнитного поля внутри соленоида, когда в него вставлен железный сердечник, магнитную проницаемость  и намагниченность J 2 сердечника (график зависимости индукции магнитного поля от напряжённости представлен на рис. 3);
и намагниченность J 2 сердечника (график зависимости индукции магнитного поля от напряжённости представлен на рис. 3);
5). построить для соленоида с сердечником график зависимости потокосцепления  от тока I в интервале 0
от тока I в интервале 0  I
I  I 1 через каждый 1 А.
I 1 через каждый 1 А.
Числовые значения параметров задачи
| № варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| l, м | 0,3 | 0,4 | 0,5 | 0,6 | 0,5 | 0,4 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,6 | 0,5 |
| D, см | 3 | 4 | 5 | 6 | 5 | 4 | 3 | 4 | 5 | 6 | 7 | 6 | 5 |
| N | 150 | 200 | 250 | 300 | 400 | 300 | 200 | 250 | 300 | 350 | 400 | 300 | 200 |
| I, А | 3 | 4 | 5 | 4 | 5 | 4 | 3 | 5 | 6 | 6 | 7 | 5 | 4 |
| I 1, А | 3 | 4 | 5 | 4 | 5 | 4 | 3 | 5 | 6 | 6 | 7 | 5 | 4 |
| № варианта | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| l, м | 1,0 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0,4 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 |
| D, см | 5 | 4 | 3 | 4 | 5 | 6 | 4 | 5 | 3 | 4 | 5 | 6 | 5 |
| N | 500 | 450 | 400 | 350 | 300 | 250 | 200 | 200 | 250 | 300 | 350 | 400 | 450 |
| I, А | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 2 | 3 | 4 |
| I 1, А | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 2 | 3 | 4 |

Рис. 3
4. В магнитном поле находится квадратная проволочная рамка со стороной l и сопротивлением R. Определить:
I. В случае однородного магнитного поля индукцией В:
1). электрический заряд q, который пройдёт через рамку, при её повороте на угол 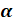 ;
;
2). ЭДС индукции  , которая возникнет в рамке в случае, если одна её сторона подвижная и перемещается перпендикулярно линиям магнитной индукции со скоростью
, которая возникнет в рамке в случае, если одна её сторона подвижная и перемещается перпендикулярно линиям магнитной индукции со скоростью 
3). среднюю ЭДС индукции < 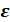 >, возникающую в рамке при включении магнитного поля в течение времени
>, возникающую в рамке при включении магнитного поля в течение времени  t, если её плоскость перпендикулярна к направлению магнитного поля;
t, если её плоскость перпендикулярна к направлению магнитного поля;
4). максимальную ЭДС индукции  , если рака равномерно вращается в магнитном поле с угловой скоростью
, если рака равномерно вращается в магнитном поле с угловой скоростью  , а ось вращения лежит в плоскости рамки и перпендикулярна линиям магнитной индукции.
, а ось вращения лежит в плоскости рамки и перпендикулярна линиям магнитной индукции.
II. Индукция магнитного поля меняется по закону В = В 0  , плоскость рамки перпендикулярна к направлению магнитного поля:
, плоскость рамки перпендикулярна к направлению магнитного поля:
5). магнитный поток Фm, пронизывающий рамку; ЭДС индукции  , возникающую в рамке; силу тока I, текущего в рамке в момент времени t.
, возникающую в рамке; силу тока I, текущего в рамке в момент времени t.
Числовые значения параметров задачи
| № варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| l, м | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,4 | 0,3 | 0,2 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| R, Ом | 2 | 1 | 3 | 4 | 5 | 4 | 3 | 2 | 2 | 1 | 3 | 4 | 5 |
| В, Тл | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 |

| 30 | 45 | 60 | 90 | 0 | 30 | 45 | 60 | 90 | 0 | 30 | 45 | 60 |
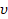 , , 
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 1 | 2 | 3 | 4 |
 t, мс t, мс
| 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 4 | 5 | 6 | 7 | 8 |
 рад. рад.
| 314 | 628 | 942 | 157 | 314 | 628 | 942 | 1256 | 157 | 314 | 628 | 942 | 1256 |
| В 0, Тл | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0.08 | 0,09 | 0,1 | 0,08 | 0,07 | 0.06 |
| t, c | 5 | 4 | 3 | 2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| № варианта | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| l, м | 0,5 | 0,6 | 0,7 | 0,5 | 0,4 | 0,3 | 0,2 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 |
| R, Ом | 5 | 6 | 7 | 5 | 4 | 3 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| В, Тл | 1,0 | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0,4 | 0,3 | 0,2 | 0,1 | 0,2 | 0,3 | 0,4 |

| 0 | 30 | 45 | 60 | 90 | 0 | 30 | 45 | 60 | 90 | 0 | 30 | 45 |
 , , 
| 10 | 9 | 8 | 7 | 6 | 5 | 3 | 2 | 1 | 2 | 3 | 4 | 5 |
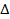 t, мс t, мс
| 10 | 9 | 8 | 7 | 6 | 5 | 3 | 2 | 1 | 2 | 3 | 4 | 5 |
 рад. рад.
| 157 | 314 | 628 | 942 | 1256 | 157 | 314 | 628 | 942 | 1256 | 157 | 314 | 628 |
| В 0, Тл | 0,08 | 0,07 | 0,06 | 0,05 | 0,04 | 0,03 | 0,02 | 0,01 | 0,02 | 0,08 | 0,07 | 0,06 | 0,05 |
| t, c | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 1 | 2 | 3 |
5. Рассматриваем систему уравнений Максвелла:
 2020-04-20
2020-04-20 207
207








