| Годы | Инвестиции в осн. капитал, млн. руб. | Взвешенная скользящая средняя | (у-ŷ)² | ||||
| 3-членная | 5-членная | 7-членная | 3-членная | 5-членная | 7-членная | ||
| 1990 | 1,80 | - | - | - | - | - | - |
| 1991 | 1,50 | 1,28667 | - | - | 0,045511 | - | - |
| 1992 | 0,56 | 0,856667 | 0,988 | - | 0,088011 | 0,183184 | - |
| 1993 | 0,51 | 0,546667 | 0,758 | 0,914286 | 0,001344 | 0,061504 | 0,163447 |
| 1994 | 0,57 | 0,576667 | 0,62 | 0,77 | 4,44E-05 | 0,0025 | 0,04 |
| 1995 | 0,65 | 0,676667 | 0,666 | 0,632857 | 0,000711 | 0,000256 | 0,000294 |
| 1996 | 0,81 | 0,75 | 0,672 | 0,654286 | 0,0036 | 0,019044 | 0,024247 |
| 1997 | 0,79 | 0,713333 | 0,7 | 0,687143 | 0,005878 | 0,0081 | 0,01058 |
| 1998 | 0,54 | 0,68 | 0,718 | 0,715714 | 0,0196 | 0,031684 | 0,030875 |
| 1999 | 0,71 | 0,663333 | 0,71 | 0,744286 | 0,002178 | 0 | 0,001176 |
| 2000 | 0,74 | 0,74 | 0,722 | 0,755714 | 0 | 0,000324 | 0,000247 |
| 2001 | 0,77 | 0,786667 | 0,792 | 0,78 | 0,000278 | 0,000484 | 0,0001 |
| 2002 | 0,85 | 0,836667 | 0,842 | 0,854286 | 0,000178 | 0,000064 | 1,84E-05 |
| 2003 | 0,89 | 0,9 | 0,906 | 0,925714 | 0,0001 | 0,000256 | 0,001276 |
| 2004 | 0,96 | 0,97 | 0,994 | 1,01429 | 0,0001 | 0,001156 | 0,002947 |
| 2005 | 1,06 | 1,07667 | 1,096 | - | 0,000278 | 0,001296 | - |
| 2006 | 1,21 | 1,21 | - | - | 0 | - | - |
| 2007 | 1,36 | - | - | - | - | - | - |
| 0,167811 | 0,309852 | 0,275206 | |||||
Сглаживание по трехчленной скользящей средней дало более сглаженный ряд, так как для трехчленной скользящей средней оказалась меньше сумма квадратов отклонений фактических данных (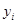 ) от сглаженных (
) от сглаженных (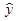 ) (
) (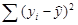 =0.167811). Иными словами, трехчленная скользящая средняя лучше всего представляет закономерность движения уровней динамического ряда.
=0.167811). Иными словами, трехчленная скользящая средняя лучше всего представляет закономерность движения уровней динамического ряда.
Для наглядности рассмотрим, как отклоняются значения тренда от фактических на графике.
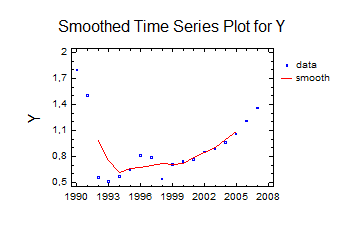
Рисунок 2.1 - График изменения инвестиционного потока, млрд. руб
Рисунок 2.1 показывает как практически полное совпадение фактических и теоретических данных после 1999 года, так и существование достаточно заметных расхождений между трендовыми значениями и реальными данными в период с 1993 по 2000 годы, в целом же трендовая тенденция инвестиционного потока в основной капитал с1990 по 2008 годы совпадает с реальностью.
Изменим метод сглаживания и рассмотрим взвешенное экспоненциальное сглаживание.
Смысл экспоненциальных средних состоит в том, чтобы найти такие средние, в которых влияние прошлых наблюдений затухает по мере удаления от момента, для которого определяются средние. Веса в экспоненциальных средних устанавливаются в виде коэффициентов 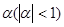 . Веса по времени убывают экспоненциально, а сумма весов стремится к 1.
. Веса по времени убывают экспоненциально, а сумма весов стремится к 1.
Экспоненциальная средняя определяется по формуле Р. Брауна:
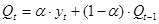 ,
,
где 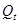 − экспоненциальная средняя (сглаженное значение уровня ряда) на момент
− экспоненциальная средняя (сглаженное значение уровня ряда) на момент 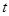 ;
;
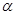 − вес текущего наблюдения при расчете экспоненциальной средней;
− вес текущего наблюдения при расчете экспоненциальной средней;
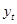 − фактический уровень динамического ряда в момент времени
− фактический уровень динамического ряда в момент времени 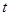 ;
;
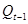 − экспоненциальная средняя предыдущего периода.
− экспоненциальная средняя предыдущего периода.
Таблица 2.2
 2020-04-20
2020-04-20 91
91








