2020-04-07
330
При задании граничных условий III рода передача тепла осуществляется между двумя теплоносителями через разделяющую стенку (см. рис. 1.5).
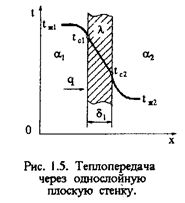
Заданы коэффициент теплопроводности λ, толщина стенки δ, коэффициенты теплоотдачи теплоносителей α1, α2 и их температуры tж1, tж2. Плотность теплового потока определяется по следующему выражению:
| (1.20) |
где k — коэффициент теплопередачи, Вт/(м2 × К).
| (1.21) |
Температуры на левой и правой поверхностях равны:
| (1.22) |
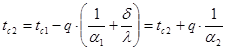
| (1.23) |
Для многослойной плоской стенки плотность теплового потока (см. рис. 1-4)
| (1.24) |
где
kм — коэффициент теплопередачи многослойной плоской стенки, Вт/(м2 × К).
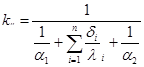
| (1.25) |
Температуры поверхностей определяются из следующих выражений:
|
| (1.26) |
| (1.27) |
| (1.28) |
В) Смешанные граничные условия
Рассмотрим случай, когда для плоской однородной стенки заданы смешанные граничные условия (второго и третьего рода).
Пусть на одну из поверхностей стенки поступает постоянный тепловой поток q = const (при x=0), а на другой поверхности заданы коэффициент теплоотдачи α2 и температура жидкости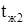 
. Внутренние источники в теле отсутствуют (см. рис. 1.6.).
Температура на поверхностях стенки и на границе слоев может быть определена по следующим уравнениям:
| (1.29) |
| (1.30) |
на поверхности между слоями m-1 и m
| (1.31) |
Распределение температуры внутри любого слоя находится по уравнению:
| (1.32) |
если коэффициент теплопроводности является функцией температуры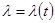 
. В противном случае, расчетная формула будет следующей:
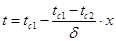
| (1.33) |
Передача тепла через цилиндрическую стенку
