2020-04-07
928
Рассмотрим математические модели для исследования динамики системы самонаведения по методу пропорциональной навигации осесимметричного ЛА с аэродинамическим управлением. ЛА стабилизирован по крену и управление осуществляется в двух взаимно-перпендикулярных плоскостях. Для реализации метода пропорциональной навигации используется ГСН с гироскопической стабилизацией.
Нелинейная модель. Движение осесимметричного ЛА с аэродинамическим управлением в пространстве, рассматриваемого как твердое тело, определяется нелинейной системой дифференциальных уравнений (2.1).
К этой системе добавим уравнения (3.1), учитывающие динамику контуров стабилизации крена, тангажа и рыскания.
К уравнениям (2.1), (3.1) добавим неравенства (3.2) и (3.3), учитывающие ограничения на углы закладки рулей и входные управляющие сигналы 
, 
.
Управляющие сигналы и формируются пропорционально ошибкам 
и :
; 
, (6.1)
где - ошибка наведения в вертикальной плоскости;
- ошибка наведения в горизонтальной плоскости;
|
|
|
, 
- коэффициенты усиления блоков формирования команд в вертикальной и боковой плоскостях;
, 
- компенсационные поправки.
Ошибки наведения в двух плоскостях по методу пропорциональной навигации определяются формулами:
, 
(6.2)
где 
- коэффициент пропорциональности в методе пропорциональной навигации.
Рассмотрим формирование ошибки и управляющих сигналов , при использовании ГСН с гироскопической стабилизацией.
В методе пропорциональной навигации должны выполняться соотношения:
, (6.3)
. (6.4)
Умножим левую и правую часть уравнения (6.3) на 
, тогда получим
.
Следовательно, сигнал на выходе ГСН, пропорциональный 
, можно использовать для формирования требуемой величины нормальной перегрузки.
Если коэффициент усиления ГСН (см. формулу (5.4)) 
, то для реализации метода пропорциональной навигации нужно сигнал с выхода ГСН умножить на коэффициент 
, выбираемый из условия
тогда
(6.5)
и сигнал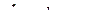 
будет равен требуемой величине нормальной перегрузки.
Если коэффициент усиления контура стабилизации перегрузки в вертикальной плоскости равен 
, то сигнал управления на входе контура стабилизации перегрузки в вертикальной плоскости определяется уравнением
, (6.6)
где 
.
Рассмотрим формирование сигнала управления в боковой плоскости.
Умножим левую и правую часть уравнения (6.4) на 
, тогда
.
Выберем коэффициент усиления ГСН при измерении 
равным 
, тогда на выходе ГСН получим сигнал
|
|
|
.
Если коэффициент усиления ГСН при измерении такой же, как при измерении , 
, то для реализации метода пропорциональной навигации сигнал нужно умножить на коэффициент , выбираемый из условия
,
тогда
(6. 7)
В этом случае сигнал будет равен требуемому значению нормальной перегрузки 
.
Если коэффициент усиления контура стабилизации перегрузки в боковой плоскости равен 
, то сигнал управления на входе контура стабилизации перегрузки в боковой плоскости определяется уравнением
(6.8)
где
.
Динамика ГСН с гироскопической стабилизацией в вертикальной плоскости определяется уравнениями (см. (5.2)):
;
; (6.9)
.
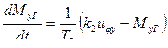Аналогичной системой уравнений определяется динамика ГСН при измерении угловой скорости 
:
;
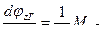; (6.10)
.
В (6.9) и (6.10) слагаемые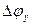 
и 
учитывают ошибки в работе чувствительного элемента ГСН. При моделировании ошибки формируются в виде случайных функций с заданными статистическими свойствами, учитывающими особенности используемых ГСН (радиолокационных, световых или тепловых).
Углы визирования цели в горизонтальной и вертикальной плоскостях определяются из решения следующей системы дифференциальных уравнений, определяющих положение цели относительно ЛА:
;
; (6.11)
.
Движение цели может задаваться в виде (3.9) или в виде системы дифференциальных уравнений (3.10).
Возмущения, действующие на ЛА, можно задавать так же, как в разделе 3.1.
Система уравнений (2.1), (3.1), (3.2), (3.3), (6.1), (6.5) - (6.11), уравнения движения цели и математические модели возмущений определяют динамику процесса самонаведения по методу пропорциональной навигации.
Рассмотрим математическую модель системы самонаведения по методу пропорциональной навигации в вертикальной плоскости.
С учетом системы уравнений (2.2) и рассмотренных математических моделей элементов системы самонаведения с гироскопической ГСН получим следующую систему уравнений:
;
;
;
;
;
;
;
;
;
;
;
;
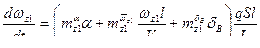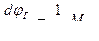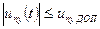; (6.12)
;
;
;
;
;
;
;
;
;
,
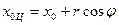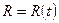где 
; 
; 
; 
; 
.
Система (6.12) записана без учета возмущений и ошибок измерений.
Аналогичную систему уравнений можно составить для исследования точности систем самонаведения по методу пропорциональной навигации в горизонтальной плоскости, когда для измерения угловой скорости линии визирования цели используется ГСН с гироскопической стабилизацией.
Линейная модель. Рассмотрим линейную модель системы самонаведения при наведении по методу пропорциональной навигации в вертикальной плоскости с использованием ГСН с гироскопической стабилизацией.
Первый этап продольного возмущенного движения ЛА определяется линейной системой дифференциальных уравнений (2.4), которой соответствуют передаточные функции (2.8). Структурная схема системы стабилизации ЛА в вертикальной плоскости приведена на рис. 2.3.
Линеаризуем кинематические уравнения, определяющие положение цели относительно ЛА:
;
. (6.13)
Линеаризация осуществляется относительно невозмущенного движения, определяемого выбранным методом наведения и заданием программы движения цели.
После линеаризации получим:
;
. (6.14)
Пусть скорости ЛА и цели изменяются в соответствии с заданным невозмущенным движением, тогда 
.
В этом случае система уравнений (6.14) станет проще:
;
(6.15)
|
|
|
Так как вариация 
не существенно влияет на динамику самонаведения при использовании метода пропорциональной навигации, то во втором уравнении опустим слагаемое 
, тогда
, (6.16)
где 
; 
;
.
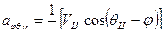Уравнение (6.16) с учетом вида коэффициентов 
, 
можно записать так
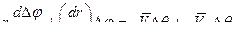, (6.17)
где 
, 
.
Если предположить, что можно использовать метод замораживания коэффициентов, тогда из (6.17) следует, что передаточная функция будет иметь следующий вид
(6.18)
где
; 
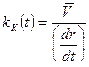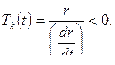
Передаточная функция (6.18) зависит от параметра 
и называется параметрической передаточной функцией.
В данном случае получаем параметрическую передаточную функцию неустойчивого апериодического звена со слабо изменяющимся передаточным коэффициентом 
и с отрицательной постоянной времени 
, стремящейся к нулю при приближении ЛА к цели.
Постоянная времени примерно равна времени полета 
, оставшемуся до полного сближения с целью.
Передаточную функцию, аналогичную (6.18), можно записать и для вариации 
, обусловленной маневром цели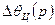 
. В этом случае нужно только в формуле для заменить 
на 
.
Следовательно, если 
, 
, 
, 
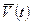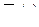являются медленно изменяющимися функциями, тогда параметрическим передаточным функциям кинематического звена соответствует структурная схема, приведенная на рис. 6.1.
При исследовании заключительного участка траектории наведения методом “замораживания“ коэффициентов можно получить очень грубые качественные ошибки.
Для повышения точности анализа в таких условиях можно преобразовать исходные уравнения с существенно переменными коэффициентами путем введения новых переменных. Эти переменные в некоторых случаях можно подобрать таким образом, что после преобразования получается уравнение с медленно изменяющимися коэффициентами. Такой прием был рассмотрен в разделе 3.5 при анализе системы телеуправления.
Кроме того, можно использовать более точные параметрические передаточной функции, учитывающие переменность коэффициентов.
|
|
|
В общем случае определение параметрической передаточной функции является сложной задачей, но в некоторых частных случаях она может быть определена сравнительно просто.
Если исходное дифференциальное уравнение системы имеет вид
то, вводя оператор дифференцирования, можно записать его более компактно:
где
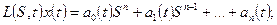
Можно показать [16], что параметрическая передаточная функция 
, отвечающая этому дифференциальному уравнению, может быть определена как любое частное решение некоторого другого линейного дифференциального уравнения, которое можно записать в следующей символической форме:
,
где 
- оператор дифференцирования по времени; 
- комплексная переменная преобразования Лапласа.
Получим эту параметрическую передаточную функцию для уравнения (6.17) при 
:
, (6.19)
где 
; 
; 
.
В операторной форме уравнение (6.19) будет иметь вид
.
Тогда для определения параметрической передаточной функции необходимо решить уравнение
или
где 
; 
, в котором переменную следует рассматривать как параметр.
Для данного дифференциального уравнения решение можно записать в виде:
,
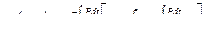где 
- константа, определяемая из начальных условий.
Принимаем 
, тогда параметрическая передаточная функция будет иметь вид:
Если 
, тогда
. (6.20)
Если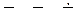 
, где 
, то
(6.21)
Обычно отношение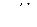 
достаточно велико и измеряется десятками секунд, поэтому в передаточную функцию входит звено с большой постоянной времени.
Это позволяет во многих случаях передаточную функцию упрощать, так как при достаточно больших частотах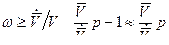 
, откуда
(6.22)
Принимая во внимание, что (6.20) и (6.22) аналогичны, формулу (6.20) параметрической передаточной функции кинематического звена можно считать довольно универсальной.
Передаточная функция кинематического звена от 
к 
имеет аналогичную форму, но с заменой на 
. На рис. 6.2 приведена структурная схема кинематического звена, соответствующая формуле (6.20).
Используя линейные математические модели ГСН с гироскопической стабилизацией, ЛА и кинематического звена составим структурную схему ССН в вертикальной плоскости при наведении по методу пропорциональной навигации, приведенную на рис.6.3.
На основании этой схемы можно выполнить ряд расчетов, связанных с исследованием качественных показателей ССН, включая исследование динамической точности.
В качестве выходной величины линейной модели ССН удобнее всего использовать мгновенный промах 
, так как он просто связан с угловой скоростью линии визирования цели 
и характеризует точность работы ССН.
За точность работы ССН следует принимать величину , вычисляемую за 0,3-0,5 с до момента максимального сближения с целью, так как в этом случае истинный промах будет мало отличаться от мгновенного промаха.
На рис. 6.3 входные воздействия 
и 
определяют движение по кинематической траектории.
При вычислении мгновенного промаха используются программные значения наклонной дальности до цели 
и ее скорости изменения 
при движении по кинематической траектории.
Для формирования ошибки наведения на рис. 6.3 используется формула (6.2), где коэффициент 
вычисляется по формуле 
, учитывающей коэффициент усиления ГСН 
Воздействие учитывает дополнительный маневр цели, отличный от принятого при расчете кинематической траектории.
Воздействие учитывает шумы, действующие на ГСН. Действие шумов на систему вызывает появление случайной составляющей ошибки наведения. Характер и уровень шумов существенно зависит от рода цели, ее размеров, типа ГСН, расстояния до цели и многих других факторов. Шум не является стационарным, он возрастает по мере сближения с целью.
Воздействие 
учитывает возмущающие силы и моменты, действующие непосредственно на ЛА.
