2020-04-07
345
Рассмотрим нелинейную модельССН в пространстве, реализующую метод прямого наведения с использованием ГСН с электромеханическим (негироскопическим) приводом.
Как и в разделе 6.1 предполагается, что ЛА стабилизирован по крену.
Отличие этой модели от математической модели самонаведения, рассмотренной в разделе 6.1, заключается в способе формирования управляющих сигналов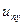 
и 
.
Сигнал управления в вертикальной плоскости формируется пропорционально сигналу 
с выхода ГСН с электромеханическим приводом (см. рис. 5.2) и определяется с учетом динамики ГСН следующими уравнениями:
; 
; 
;
; 
; 
; 
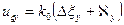. (6.23)
Аналогичная система уравнений определяет формирование сигнала управления в горизонтальной плоскости:
; 
; 
;
; 
; 
; 
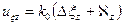. (6.24)
где 
- угол рыскания, а 
- угол визирования цели в вертикальной плоскости.
Соотношение между углами в горизонтальной плоскости показано на рис. 6.4.
Рассмотрим математическую модель для исследования динамики ССН по методу прямого наведения в горизонтальной плоскости с использованием ГСН с электромеханическим приводом.
|
|
|
С учетом системы уравнений (2.3) и рассмотренных математических моделей элементов ССН получим следующую систему уравнений:
1. 
;
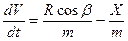2. 
;
3. 
;
4. 
;
5. 
;
6. 
;
7. 
;
8. 
;
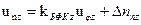9. ;
10. ; (6.25)
11. 
;
12. 
;
13. ;
14. 
;
15. 
;
16. 
;
17. 
;
18. 
;
19. 
;
20. 
;
21. 
;
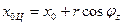22. 
;
23. 
;
24. 
,
где 
; 
; 
; 
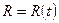- ошибка на выходе чувствительного элемента ГСН.
